Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) có \(\widehat B = {70^0},\widehat C = {35^0},AC = 4,5cm.\) Diện tích tam giác \(ABC\) gần nhất với giá trị nào dưới đây? (làm tròn đến chữ số thập phân thứ hai)
Trả lời bởi giáo viên
Đáp án đúng: c
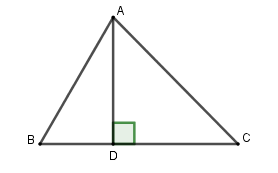
Kẻ đường cao \(AD\).
Xét tam giác vuông \(ACD\), có \(AD = AC.\sin C = 4,5.\sin 35^\circ \approx 2,58\,cm\); \(CD = AC.\cos C = 4,5.\cos 35^\circ \approx 3,69\,cm\)
Xét tam giác vuông \(ABD\), có \(BD = AD.\cot B \approx 2,58.\cot 70^\circ \approx 0,94\,cm\)
Suy ra \(BC = BD + DC = 0,94 + 3,69 = 4,63\)
Do đó \({S_{ABC}} = \dfrac{{AD.BC}}{2} \approx 5,97\)\(c{m^2}\).
Hướng dẫn giải:
+) Kẻ đường cao \(AD\)
+) Sử dụng hệ thức giữa cạnh và góc trong tam giác vuông thích hợp và định lý Py-ta-go để tính cạnh.
+) Sử dụng công thức tính diện tích tam giác.
Câu hỏi khác
- Bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông toán 9 có lời giải
- Bài tập một số hệ thức về cạnh và góc trong tam giác vuông toán 9 có lời giải
- Bài tập tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập ứng dụng thực tế tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập hay và khó chương hệ thức lượng trong tam giác vuông toán 9 có lời giải
