Cho tứ giác \(ABCD\) có \(\widehat A = \widehat D = {90^0},\widehat C = {45^0},AB = 6cm,AD = 8cm.\) Tính diện tích tứ giác \(ABCD.\)

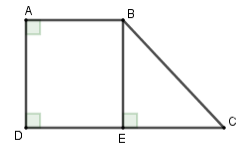
Vì \(\widehat A = \widehat D = {90^0} \Rightarrow AD{\rm{//}}BC\) hay \(ABCD\) là hình thang vuông tại \(A,D\)

Kẻ \(BE \bot DC\) tại \(E\).

Tứ giác \(ABED\) có ba góc vuông \(\widehat A = \widehat D = \widehat E = 90^\circ \) nên \(ABED\) là hình chữ nhật

Suy ra \(DE = AB = 6\,\,cm;BE = AD = 8\,cm\)

Xét tam giác \(BEC\) vuông tại \(E\) có \(\widehat {BCE} = 45^\circ \) nên tam giác \(BEC\) vuông cân tại \(E\) \( \Rightarrow EC = BE = 8cm \Rightarrow DC = DE + EC = 6 + 8 = 14cm\)

Do đó \({S_{ABCD}} = \dfrac{{\left( {AB + CD} \right).AD}}{2} = \dfrac{{\left( {6 + 14} \right)8}}{2} = 80\,\,c{m^2}\).