Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) có \(AB = 12,AC = 15\) và \(\widehat B = {60^0}\). Tính \(BC\)
Trả lời bởi giáo viên
Đáp án đúng: b
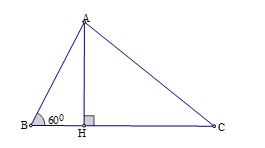
Kẻ đường cao \(AH\).
Xét tam giác vuông \(ABH\), ta có: \(BH = AB.\cos B = AB.\cos {60^0} = 12.\dfrac{1}{2} = 6\)\(AH = AB.\sin B = AB.\sin {60^0} = 12.\dfrac{{\sqrt 3 }}{2} = 6\sqrt 3 \).
Áp dụng định lý Pythago vào tam giác vuông \(AHC\) ta có:
\(H{C^2} = A{C^2} - A{H^2} = {15^2} - {\left( {6\sqrt 3 } \right)^2} = 117\). Suy ra \(HC = 3\sqrt {13} \). Vậy \(BC = CH + HB = 3\sqrt {13} + 6\).
Hướng dẫn giải:
+) Kẻ đường cao \(AH\)
+) Sử dụng hệ thức giữa cạnh và góc trong tam giác vuông thích hợp và định lý Py-ta-go để tính cạnh.
Câu hỏi khác
- Bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông toán 9 có lời giải
- Bài tập một số hệ thức về cạnh và góc trong tam giác vuông toán 9 có lời giải
- Bài tập tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập ứng dụng thực tế tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập hay và khó chương hệ thức lượng trong tam giác vuông toán 9 có lời giải
