Cho tam giác \(ABC\) cân tại \(A,\,\,\angle B = {65^0},\)  đường cao \(CH = 3,6\).  Hãy giải tam giác \(ABC\).

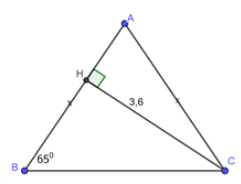
Vì \(\Delta ABC\) là tam giác cân tại \(A\)\( \Rightarrow \angle C = \angle B = {65^0}\)

Ta có \(\angle A + \angle B + \angle C = {180^0}\)(định lý tổng ba góc trong một tam giác)

\( \Rightarrow \angle A = {180^0} - 2\angle C = {180^0} - {2.65^0} = {50^0}\)

Xét \(\Delta ACH\) vuông tại \(H\) ta có:

\(\sin A = \dfrac{{CH}}{{AC}}\) \( \Leftrightarrow \sin {50^0} = \dfrac{{3,6}}{{AC}}\)\( \Rightarrow AC = \dfrac{{3,6}}{{\sin {{50}^0}}} \approx 4,7\)

Vì \(\Delta ABC\) là tam giác cân tại \(A\)\( \Rightarrow AC = AB \approx 4,7\)

Xét \(\Delta BCH\) vuông tại \(H\) ta có:

\(\sin B = \dfrac{{CH}}{{BC}} \Leftrightarrow \sin {65^0} = \dfrac{{3,6}}{{BC}} \)\(\Rightarrow BC = \dfrac{{3,6}}{{\sin {{65}^0}}} \approx 3,97\)