Tính diện tích tứ giác \(DENM\)
Vì \(DM \bot DE;EN \bot DE \Rightarrow DM{\rm{//}}EN;\widehat D = \widehat E = 90^\circ \) nên \(DENM\) là hình thang vuông
Theo câu các câu trước ta có: \(DM = \dfrac{{BH}}{2} = 4,5;EN = \dfrac{{CH}}{2} = 8;DE = 12\)
Nên \({S_{DENM}} = \dfrac{{\left( {DM + EN} \right).DE}}{2} = \dfrac{{\left( {4,5 + 8} \right).12}}{2} = 75\,c{m^2}\)
Tính độ dài đoạn MN?.
+) Ta có \(\widehat {NEC} + \widehat {AED} = 90^\circ \) mà \(\widehat {AED} = \widehat {HAE}\) (do \(AEHD\) là hình chữ nhật) và \(\widehat {HAE} = \widehat {ABC}\) (cùng phụ với \(\widehat {ACB}\)) nên \(\widehat {NEC} + \widehat {ABC} = 90^\circ \) mà \(\widehat {ACB} + \widehat {ABC} = 90^\circ \) nên \(\widehat {ACB} = \widehat {NEC}\) hay \(\Delta NEC\) cân tại \(N\)\( \Rightarrow EN = NC\).\(\left( 1 \right)\)
+) \(\widehat {NEC} + \widehat {HEN} = 90^\circ \) mà \(\widehat {NEC} = \widehat {NCE} \Rightarrow \widehat {NCE} + \widehat {HEN} = 90^\circ \), lại có \(\widehat {NCE} + \widehat {NHE} = 90^\circ \) nên \(\widehat {NEH} = \widehat {NHE}\) hay \(\Delta NEH\) cân tại \(N\) suy ra \(NE = NH\), \(\left( 2 \right)\)
Từ \(\left( 1 \right);\left( 2 \right)\) ta có \(NH = NC\)
Tương tự ta có \(MH = MB\) nên \(MN = MH + NH = \dfrac{1}{2}HB + \dfrac{1}{2}HC = \dfrac{1}{2}.9 + \dfrac{1}{2}.16 = 12,5cm\).
Tính độ dài đoạn thẳng \(DE\).
Tứ giác \(AEHD\) là hình chữ nhật vì \(\widehat A = \widehat E = \widehat D = 90^\circ \) nên \(DE = AH\)
Xét \(\Delta ABC\) vuông tại \(A\) có \(A{H^2} = HB.HC\)\( = 9.16 = 144 \Rightarrow AH = 12\)
Nên \(DE = 12\,cm\).
Tính độ dài đoạn thẳng \(DE\).
Tứ giác \(AEHD\) là hình chữ nhật vì \(\widehat A = \widehat E = \widehat D = 90^\circ \) nên \(DE = AH\)
Xét \(\Delta ABC\) vuông tại \(A\) có \(A{H^2} = HB.HC\)\( = 9.16 = 144 \Rightarrow AH = 12\)
Nên \(DE = 12\,cm\).
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ (như hình vẽ). Hệ thức nào sau đây là đúng?
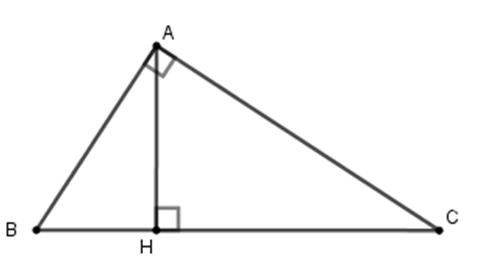
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Khi đó ta có hệ thức $H{A^2} = HB.HC$
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ (như hình vẽ). Hệ thức nào sau đây là sai?
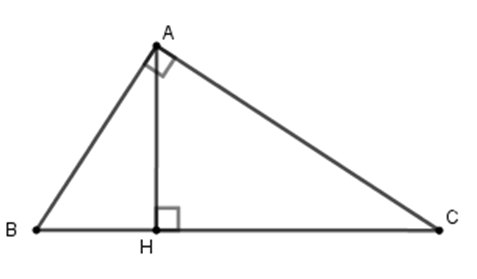
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Khi đó ta có các hệ thức
$A{C^2} = CH.BC$; $A{B^2} = BH.BC$; $AB.AC = BC.AH$và $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$
Nhận thấy phương án D: $A{H^2} = \dfrac{{A{B^2} + A{C^2}}}{{A{B^2}.A{C^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$ là sai.
Tính $x,y$ trong hình vẽ sau:
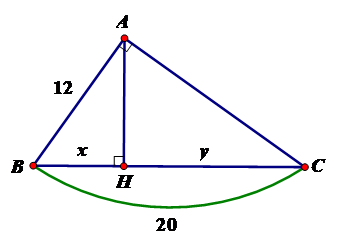
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
$A{B^2} = BH.BC \Leftrightarrow BH = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{144}}{{20}} = 7,2$$ \Rightarrow CH = BC - BH = 20 - 7,2 = 12,8$
Vậy $x = 7,2;y = 12,8$
Tính $x$ trong hình vẽ sau (làm tròn đến chữ số thập phân thứ hai)
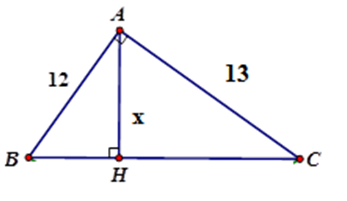
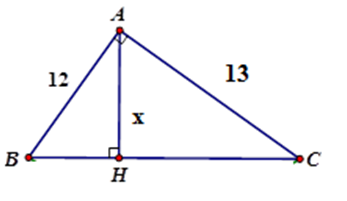
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông $ABC$ ta có:
$\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$
\( \Leftrightarrow \dfrac{1}{{A{H^2}}} = \dfrac{{A{B^2} + A{C^2}}}{{A{B^2}.A{C^2}}} \)\(\Leftrightarrow A{H^2} = \dfrac{{A{B^2}.A{C^2}}}{{A{B^2} + A{C^2} }}\)
$ \Rightarrow AH = \dfrac{{AB.AC}}{{\sqrt {A{B^2} + A{C^2}} }} = \dfrac{{12.13}}{{\sqrt {{{12}^2} + {{13}^2}} }} \approx 8,82$
Vậy $x \approx 8,82$.
Tính $x,y$ trong hình vẽ sau:
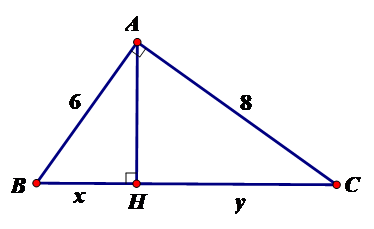
Theo định lý Pytago ta có $B{C^2} = A{B^2} + A{C^2} \Leftrightarrow B{C^2} = 100 \Leftrightarrow BC = 10$
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
$A{B^2} = BH.BC \Rightarrow BH = \dfrac{{A{B^2}}}{{BC}} $
$= \dfrac{{{6^2}}}{10} = 3,6$ hay $x = 3,6$
$ \Rightarrow CH = BC - BH $$= 10 - 3,6 = 6,4.$
hay $y = 6,4$.
Vậy $x = 3,6;y = 6,4.$
Tính $x,y$ trong hình vẽ sau:
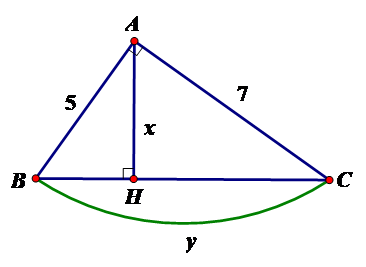
Theo định lý Pytago ta có $B{C^2} = A{B^2} + A{C^2} \Leftrightarrow B{C^2} = 74 \Leftrightarrow BC = \sqrt {74} $
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
$AH.BC = AB.AC \Leftrightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{5.7}}{{\sqrt {74} }} = \dfrac{{35\sqrt {74} }}{{74}}$
Vậy $x = \dfrac{{35\sqrt {74} }}{{74}};y = \sqrt {74} $
Cho tam giác $ABC$ vuông tại $A$, $AH \bot BC$( $H$ thuộc $BC$ ). Cho biết $AB:AC = 3:4$ và $BC = 15cm.$ Tính độ dài đoạn thẳng $BH$.
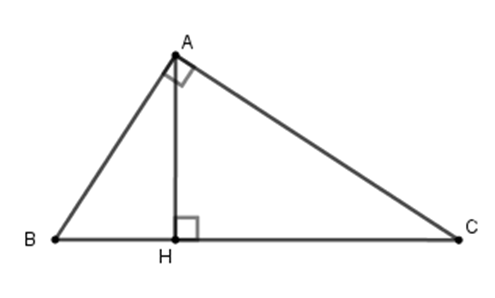
Ta có $AB:AC = 3:4$$ \Leftrightarrow \dfrac{{AB}}{3} = \dfrac{{AC}}{4} \Rightarrow \dfrac{{A{B^2}}}{9} = \dfrac{{A{C^2}}}{{16}} $$= \dfrac{{A{B^2} + A{C^2}}}{{9+16}}= \dfrac{{A{B^2} + A{C^2}}}{{25}}$ $=\dfrac{{B{C^2}}}{{25}}$$= \dfrac{{225}}{{25}} = 9$
(Vì theo định lý Pytago ta có $A{B^2} + A{C^2} = B{C^2} \Leftrightarrow A{B^2} + A{C^2} = 225$)
Nên $\dfrac{{A{B^2}}}{9} = 9 \Rightarrow AB = 9$; $\dfrac{{A{C^2}}}{{16}} = 9 \Rightarrow AC = 12$
Theo hệ thức lượng trong tam giác vuông $ABC$ ta có $A{B^2} = BH.BC \Rightarrow BH = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{81}}{{15}} = 5,4$
Vậy $BH = 5,4$.
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH.$ Cho biết $AB:AC = 3:4$ và $AH = 6cm.$ Tính độ dài các đoạn thẳng $CH.$
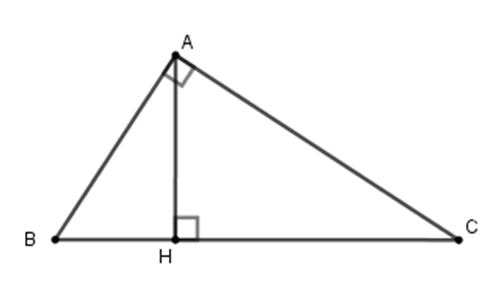
Ta có $AB:AC = 3:4$ , đặt $AB = 3a;AC = 4a\,\left( {a > 0} \right)$
Theo hệ thức lượng $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$$ \Rightarrow \dfrac{1}{{36}} = \dfrac{1}{{9{a^2}}} + \dfrac{1}{{16{a^2}}} \Rightarrow \dfrac{1}{{36}} = \dfrac{{25}}{{144{a^2}}} \Rightarrow a = \dfrac{5}{2}$ (TM )
$ \Rightarrow AB = 7,5;AC = 10$
Theo định lý Pytago cho tam giác vuông $AHC$ ta có $CH = \sqrt {A{C^2} - A{H^2}} = \sqrt {100 - 36} = 8$
Vậy $CH = 8$.
Tính $x,y$ trong hình vẽ sau:
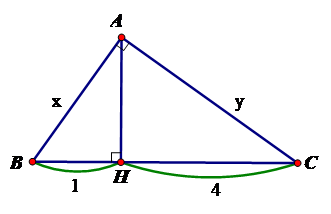
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
$A{H^2} = BH.CH$$ \Rightarrow A{H^2} = 1.4 \Rightarrow AH = 2$
Áp dụng định lý Pytago cho tam giác vuông $AHB;AHC$ ta có
$AB = \sqrt {A{H^2} + H{B^2}} = \sqrt 5 ;AC = \sqrt {A{H^2} + H{C^2}} = 2\sqrt 5 $
Vậy $x = \sqrt 5 ;y = 2\sqrt 5 $.
Tính $x$ trong hình vẽ sau:
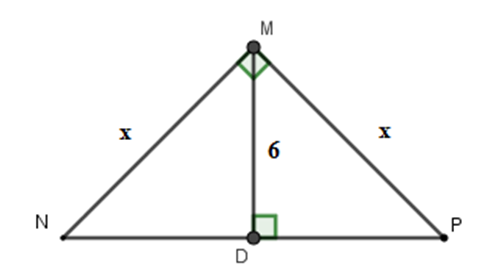
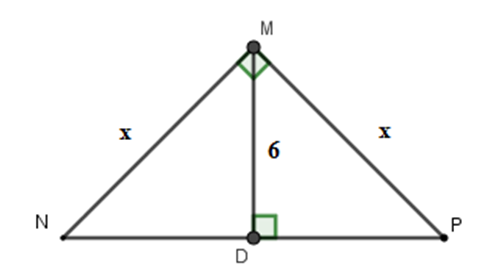
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
$\dfrac{1}{{M{D^2}}} = \dfrac{1}{{M{N^2}}} + \dfrac{1}{{M{P^2}}}$$ \Rightarrow \dfrac{1}{{36}} = \dfrac{1}{{{x^2}}} + \dfrac{1}{{{x^2}}} \Leftrightarrow \dfrac{1}{{36}} = \dfrac{2}{{{x^2}}} \Rightarrow {x^2} = 72 \Leftrightarrow x = 6\sqrt 2 $
Vậy $x = 6\sqrt 2 $.
Cho ABCD là hình thang vuông tại $A$ và $D.$Đường chéo $BD$ vuông góc với $BC.$ Biết $AD = 12cm,DC = 25cm$ . Tính độ dài $BC$, biết $BC < 20$
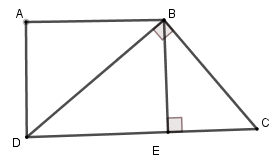
Kẻ $BE \bot CD$ tại $E$
Suy ra tứ giác $ABED$ là hình chữ nhật (vì $\widehat A = \widehat D = \widehat E = 90^\circ $) nên $BE = AD = 12\,\,cm$
Đặt $EC = x\,\left( {0 < x < 25} \right)$ thì $DE = 25 - x$
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông $BCD$ ta có
$B{E^2} = ED.EC \Leftrightarrow x\left( {25 - x} \right) = 144 $$\Leftrightarrow {x^2} - 25x + 144 = 0$ \( \Leftrightarrow {x^2} - 16x - 9x + 144 = 0 \)\(\Leftrightarrow x\left( {x - 16} \right) - 9\left( {x - 16} \right) = 0\)$\Leftrightarrow \left( {x - 16} \right)\left( {x - 9} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 16\\x = 9\end{array} \right.$(thỏa mãn)
Với $EC = 16$, theo định lý Pytago ta có $BC = \sqrt {B{E^2} + E{C^2}} = \sqrt {{{12}^2} + {{16}^2}} = 20$ (loại)
Với $EC = 9$, theo định lý Pytago ta có $BC = \sqrt {B{E^2} + E{C^2}} = \sqrt {{{12}^2} + {9^2}} = 15$ (nhận)
Vậy $BC = 15\,cm$.
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Biết \(AB:AC = 3:4\) và \(AB + AC = 21cm\).
Tính các cạnh của tam giác \(ABC\).
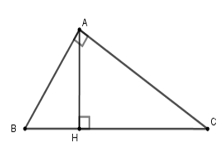
Theo giả thiết: \(AB:AC = 3:4\),
suy ra \(\dfrac{{AB}}{3} = \dfrac{{AC}}{4} = \dfrac{{AB + AC}}{{3 + 4}} = 3\). Do đó \(AB = 3.3 = 9\)\(\left( {cm} \right)\); \(AC = 3.4 = 12\left( {cm} \right)\).
Tam giác \(ABC\) vuông tại \(A\), theo định lý Py-ta-go ta có:
\(B{C^2} = A{B^2} + A{C^2} \)\(= {9^2} + {12^2} = 225\), suy ra \(BC = 15cm\).
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Biết \(AB:AC = 3:4\) và \(AB + AC = 21cm\).
Tính độ dài các đoạn \(AH,BH,CH\).
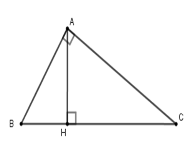
Ta có $AB = 9;AC = 12;BC = 15$
$ \Rightarrow AH.BC = AB.AC \Rightarrow AH = \dfrac{{AB.AC}}{{BC}}$$ = \dfrac{{12.9}}{{15}} = 7,2$ $A{B^2} = BH.BC \Rightarrow BH $$= \dfrac{{A{B^2}}}{{BC}} $$= \dfrac{{81}}{{15}} = 5,4$
$ \Rightarrow CH = BC - BH = 15 - 5,4 = 9,6$
Vậy $AH = 7,2;BH = 5,4;CH = 9,6$.
Cho tam giác $ABC$ vuông tại $A,$ đường cao $AH.$ Gọi $D$ và $E$ lần lượt là hình chiếu vuông góc của $H$ trên $AB, AC.$(hình vẽ)
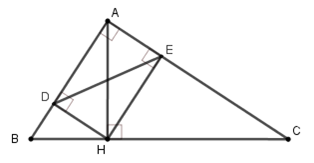
Tỉ số $\dfrac{{A{B^2}}}{{A{C^2}}}$ bằng với tỉ số nào sau đây?
Xét tam giác vuông $ABC$ có $AH$ là đường cao nên $A{B^2} = BH.BC;A{C^2} = CH.BC$
Nên $\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{BH.BC}}{{CH.BC}} = \dfrac{{HB}}{{HC}}$
Cho tam giác $ABC$ vuông tại $A,$ đường cao $AH.$ Gọi $D$ và $E$ lần lượt là hình chiếu vuông góc của $H$ trên $AB, AC.$(hình vẽ)

Tỉ số $\dfrac{{A{B^3}}}{{A{C^3}}}$ bằng với tỉ số nào sau đây?
Tam giác vuông $AHB$ có $B{H^2} = BD.AB \Rightarrow BD = \dfrac{{B{H^2}}}{{AB}}$
Tam giác vuông $AHC$ có $H{C^2} = AC.EC \Rightarrow EC = \dfrac{{H{C^2}}}{{AC}}$
Từ đó $\dfrac{{BD}}{{EC}} = \dfrac{{H{B^2}}}{{AB}}:\dfrac{{H{C^2}}}{{AC}} = \dfrac{{H{B^2}}}{{H{C^2}}}.\dfrac{{AC}}{{AB}}$ mà theo câu trước thì $\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{HB}}{{HC}}$ nên $\dfrac{{BD}}{{EC}} = \dfrac{{A{B^4}}}{{A{C^4}}}.\dfrac{{AC}}{{AB}} \Leftrightarrow \dfrac{{BD}}{{EC}} = \dfrac{{A{B^3}}}{{A{C^3}}}$
Cho tam giác $ABC$ vuông tại $A$ , đường cao $AH$ . Cho biết $BH = 4cm,CH = 9cm$. Gọi $D,E$ lần lượt là hình chiếu vuông góc của $H$ trên các cạnh $AB$ và $AC$. Các đường thẳng vuông góc với $DE$ tại $D$ và $E$ lần lượt cắt $BC$ tại $M,N$ . (hình vẽ)
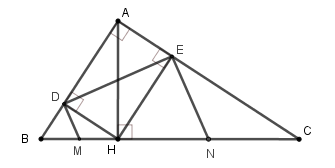
Tính độ dài đoạn thẳng $DE$.
Tứ giác $AEHD$ là hình chữ nhật vì $\widehat A = \widehat E = \widehat D = 90^\circ $ nên $DE = AH$
Xét $\Delta ABC$ vuông tại $A$ có $A{H^2} = HB.HC$$ = 4.9 = 36 \Rightarrow AH = 6$
Nên $DE = 6\,cm$.

