Cho ABCD là hình thang vuông tại $A$ và $D.$Đường chéo $BD$ vuông góc với $BC.$ Biết $AD = 12cm,DC = 25cm$ . Tính độ dài $BC$, biết $BC < 20$

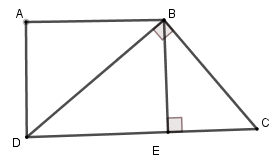
Kẻ $BE \bot CD$ tại $E$

Suy ra tứ giác $ABED$ là hình chữ nhật (vì $\widehat A = \widehat D = \widehat E = 90^\circ $) nên $BE = AD = 12\,\,cm$

Đặt $EC = x\,\left( {0 < x < 25} \right)$ thì $DE = 25 - x$

Áp dụng hệ thức giữa cạnh và đường cao trong  tam giác vuông $BCD$ ta có

$B{E^2} = ED.EC \Leftrightarrow x\left( {25 - x} \right) = 144 $$\Leftrightarrow {x^2} - 25x + 144 = 0$ \( \Leftrightarrow {x^2} - 16x - 9x + 144 = 0 \)\(\Leftrightarrow x\left( {x - 16} \right) - 9\left( {x - 16} \right) = 0\)$\Leftrightarrow \left( {x - 16} \right)\left( {x - 9} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 16\\x = 9\end{array} \right.$(thỏa mãn)

Với $EC = 16$, theo định lý Pytago ta có $BC = \sqrt {B{E^2} + E{C^2}}  = \sqrt {{{12}^2} + {{16}^2}}  = 20$ (loại)

Với $EC = 9$, theo định lý Pytago ta có $BC = \sqrt {B{E^2} + E{C^2}}  = \sqrt {{{12}^2} + {9^2}}  = 15$ (nhận)

Vậy $BC = 15\,cm$.