Câu hỏi:
2 năm trước
Cho tam giác $ABC$ vuông tại $A$ , đường cao $AH$ . Cho biết $BH = 4cm,CH = 9cm$. Gọi $D,E$ lần lượt là hình chiếu vuông góc của $H$ trên các cạnh $AB$ và $AC$. Các đường thẳng vuông góc với $DE$ tại $D$ và $E$ lần lượt cắt $BC$ tại $M,N$ . (hình vẽ)
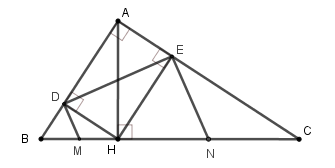
Tính độ dài đoạn thẳng $DE$.
Trả lời bởi giáo viên
Đáp án đúng: d
Tứ giác $AEHD$ là hình chữ nhật vì $\widehat A = \widehat E = \widehat D = 90^\circ $ nên $DE = AH$
Xét $\Delta ABC$ vuông tại $A$ có $A{H^2} = HB.HC$$ = 4.9 = 36 \Rightarrow AH = 6$
Nên $DE = 6\,cm$.
Hướng dẫn giải:
Bước 1: Chứng minh $DE = AH$
Bước 2: Sử dụng hệ thức $A{H^2} = BH.CH$ từ đó tính $AH$$ \Rightarrow DE$.
Câu hỏi khác
- Bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông toán 9 có lời giải
- Bài tập một số hệ thức về cạnh và góc trong tam giác vuông toán 9 có lời giải
- Bài tập tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập ứng dụng thực tế tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập hay và khó chương hệ thức lượng trong tam giác vuông toán 9 có lời giải
