Câu hỏi:
2 năm trước
Cho tam giác $ABC$ vuông tại $A,$ đường cao $AH.$ Gọi $D$ và $E$ lần lượt là hình chiếu vuông góc của $H$ trên $AB, AC.$(hình vẽ)
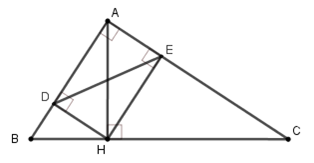
Tỉ số $\dfrac{{A{B^3}}}{{A{C^3}}}$ bằng với tỉ số nào sau đây?
Trả lời bởi giáo viên
Đáp án đúng: a
Tam giác vuông $AHB$ có $B{H^2} = BD.AB \Rightarrow BD = \dfrac{{B{H^2}}}{{AB}}$
Tam giác vuông $AHC$ có $H{C^2} = AC.EC \Rightarrow EC = \dfrac{{H{C^2}}}{{AC}}$
Từ đó $\dfrac{{BD}}{{EC}} = \dfrac{{H{B^2}}}{{AB}}:\dfrac{{H{C^2}}}{{AC}} = \dfrac{{H{B^2}}}{{H{C^2}}}.\dfrac{{AC}}{{AB}}$ mà theo câu trước thì $\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{HB}}{{HC}}$ nên $\dfrac{{BD}}{{EC}} = \dfrac{{A{B^4}}}{{A{C^4}}}.\dfrac{{AC}}{{AB}} \Leftrightarrow \dfrac{{BD}}{{EC}} = \dfrac{{A{B^3}}}{{A{C^3}}}$
Câu hỏi khác
- Bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông toán 9 có lời giải
- Bài tập một số hệ thức về cạnh và góc trong tam giác vuông toán 9 có lời giải
- Bài tập tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập ứng dụng thực tế tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập hay và khó chương hệ thức lượng trong tam giác vuông toán 9 có lời giải
