Tích $CD.CM$ bằng
Tam giác $CHD$ vuông tại $H$, ta có $C{H^2} = CM.CD$
Tam giác $CHE$ vuông tại $H$, ta có $C{H^2} = CN.CE$
Nên $CM.CD = CN.CE$.
Tích $CD.CM$ bằng
Tam giác $CHD$ vuông tại $H$, ta có $C{H^2} = CM.CD$
Tam giác $CHE$ vuông tại $H$, ta có $C{H^2} = CN.CE$
Nên $CM.CD = CN.CE$.
Tính các cạnh của tam giác \(ABC\).
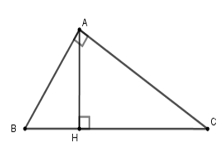
Theo giả thiết: \(AB:AC = 3:4\),
suy ra \(\dfrac{{AB}}{3} = \dfrac{{AC}}{4} = \dfrac{{AB + AC}}{{3 + 4}} = 3\). Do đó \(AB = 3.3 = 9\)\(\left( {cm} \right)\); \(AC = 3.4 = 12\left( {cm} \right)\).
Tam giác \(ABC\) vuông tại \(A\), theo định lý Py-ta-go ta có:
\(B{C^2} = A{B^2} + A{C^2} \)\(= {9^2} + {12^2} = 225\), suy ra \(BC = 15cm\).
Tỉ số $\dfrac{{A{B^2}}}{{A{C^2}}}$ bằng với tỉ số nào sau đây?
Xét tam giác vuông $ABC$ có $AH$ là đường cao nên $A{B^2} = BH.BC;A{C^2} = CH.BC$
Nên $\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{BH.BC}}{{CH.BC}} = \dfrac{{HB}}{{HC}}$
Tính độ dài đoạn thẳng $DE$.
Tứ giác $AEHD$ là hình chữ nhật vì $\widehat A = \widehat E = \widehat D = 90^\circ $ nên $DE = AH$
Xét $\Delta ABC$ vuông tại $A$ có $A{H^2} = HB.HC$$ = 4.9 = 36 \Rightarrow AH = 6$
Nên $DE = 6\,cm$.
Tích $CD.CM$ bằng
Tam giác $CHD$ vuông tại $H$, ta có $C{H^2} = CM.CD$
Tam giác $CHE$ vuông tại $H$, ta có $C{H^2} = CN.CE$
Nên $CM.CD = CN.CE$.
“Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng …” . Cụm từ thích hợp điền vào chỗ trống là
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Khi đó ta có hệ thức \(H{A^2} = HB.HC\)
Hay “Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng Tích hai hình chiếu của hai cạnh gọc vuông trên cạnh huyền”
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\) (như hình vẽ). Hệ thức nào sau đây là sai?
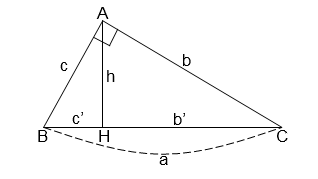
Nhận thấy \(ah = bc\) nên phương án C là sai.
Tính \(x,y\) trong hình vẽ sau:
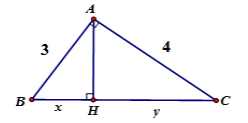
Theo định lý Pytago ta có \(B{C^2} = A{B^2} + A{C^2} \Leftrightarrow B{C^2} = 25 \Leftrightarrow BC = 5\)
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
\(A{B^2} = BH.BC \Rightarrow BH = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{{3^2}}}{5} = 1,8\) hay \(x = 1,8\)
\( \Rightarrow CH = BC - BH = 5 - 1,8 = 3,2\) hay \(y = 3,2\).
Vậy \(x = 1,8;y = 3,2\)
Cho tam giác \(ABC\) vuông tại \(A,\) chiều cao \(AH\) và \(AB = 5;AC = 12.\) Đặt \(BC = y;AH = x.\) Tính \(x,y.\)
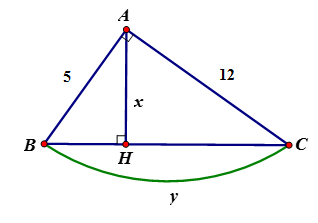
Theo định lý Pytago ta có \(B{C^2} = A{B^2} + A{C^2} \Leftrightarrow B{C^2} = 169 \Leftrightarrow BC = 13\)
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
\(AH.BC = AB.AC \Leftrightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{5.12}}{{13}} = \dfrac{{60}}{{13}}\)
Vậy \(x = \dfrac{{60}}{{13}};y = 13\)
Tính độ dài các đoạn \(AH,BH,CH\). (làm tròn đến chữ số thập phân thứ hai)
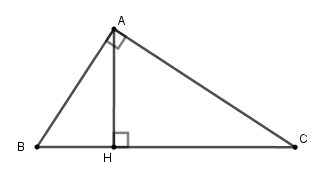
Theo câu trước ta có \(AB = 10;AC = 24;BC = 26\)
\( \Rightarrow AH.BC = AB.AC \Rightarrow AH = \dfrac{{AB.AC}}{{BC}} \)\(= \dfrac{{10.24}}{{26}} \approx 9,23;\) \(A{B^2} = BH.BC \Rightarrow BH = \dfrac{{A{B^2}}}{{BC}} \)\(= \dfrac{{{{10}^2}}}{{13}} = \dfrac{{100}}{{13}} \approx 7,69\)
\( \Rightarrow CH = BC - BH \)\(= 26 - 7,69 = 18,31\)
Vậy \(AH \approx 9,23;\)\(BH \approx 7,69;CH \approx 18,31\).
Tính các cạnh của tam giác \(ABC\).
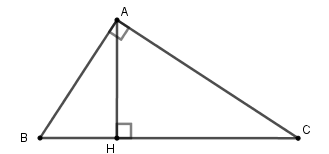
Theo giả thiết: \(AB:AC = 5:12\),
suy ra \(\dfrac{{AB}}{5} = \dfrac{{AC}}{{12}} = \dfrac{{AB + AC}}{{5 + 12}} \)\(= \dfrac{{34}}{{17}} = 2\). Do đó \(AB = 5.2 = 10\)\(\left( {cm} \right)\); \(AC = 2.12 = 24\left( {cm} \right).\)
Tam giác \(ABC\) vuông tại \(A\), theo định lý Py-ta-go ta có:
\(B{C^2} = A{B^2} + A{C^2} = {10^2} + {24^2} = 676\), suy ra \(BC = 26cm\).
Tính các cạnh của tam giác \(ABC\).

Theo giả thiết: \(AB:AC = 5:12\),
suy ra \(\dfrac{{AB}}{5} = \dfrac{{AC}}{{12}} = \dfrac{{AB + AC}}{{5 + 12}} \)\(= \dfrac{{34}}{{17}} = 2\). Do đó \(AB = 5.2 = 10\)\(\left( {cm} \right)\); \(AC = 2.12 = 24\left( {cm} \right).\)
Tam giác \(ABC\) vuông tại \(A\), theo định lý Py-ta-go ta có:
\(B{C^2} = A{B^2} + A{C^2} = {10^2} + {24^2} = 676\), suy ra \(BC = 26cm\).
Cho tam giác \(ABC\) vuông tại \(A\), \(AH \bot BC\)( \(H\) thuộc BC ). Cho biết \(AB:AC = 4:5\) và \(BC = \sqrt {41} cm.\) Tính độ dài đoạn thẳng \(CH\) (làm tròn đến chữ số thập phân thứ nhất).
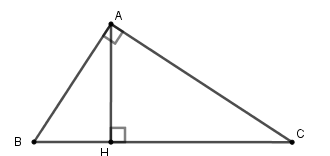
Ta có \(AB:AC = 4:5\)\( \Leftrightarrow \dfrac{{AB}}{4} = \dfrac{{AC}}{5} \Rightarrow \dfrac{{A{B^2}}}{{16}} = \dfrac{{A{C^2}}}{{25}} = \dfrac{{A{B^2} + A{C^2}}}{{16 + 25}} = \dfrac{{41}}{{41}} = 1\)
(Vì theo định lý Pytago ta có \(A{B^2} + A{C^2} = B{C^2} \Leftrightarrow A{B^2} + A{C^2} = {\left( {\sqrt {41} } \right)^2} = 41)\)
Nên \(\dfrac{{A{B^2}}}{{16}} = 1 \Rightarrow A{B^2} = 16 \Rightarrow AB = 4\); \(\dfrac{{A{C^2}}}{{25}} = 1 \Rightarrow AC = 5\)
Theo hệ thức lượng trong tam giác vuông \(ABC\) ta có \(A{C^2} = CH.BC \Rightarrow CH = \dfrac{{A{C^2}}}{{BC}} = \dfrac{{25}}{{\sqrt {41} }} \approx 3,9\)
Vậy \(CH \approx 3,9\).
Tính \(x,y\) trong hình vẽ sau:
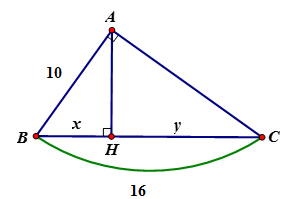
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
\(A{B^2} = BH.BC \Leftrightarrow BH = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{100}}{{16}} = 6,25\) \( \Rightarrow CH = BC - BH = 16 - 6,25 = 9,75\)
Vậy \(x = 6,25;y = 9,75\)
Tính \(x\) trong hình vẽ sau:
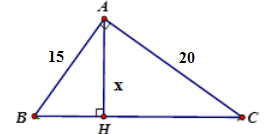
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\)\( \Rightarrow AH = \dfrac{{AB.AC}}{{\sqrt {A{B^2} + A{C^2}} }} = \dfrac{{15.20}}{{\sqrt {{{15}^2} + {{20}^2}} }} = 12\)
Vậy \(x = 12\).
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH.\) Cho biết \(AB:AC = 3:7\) và \(AH = 42cm.\) Tính độ dài đoạn thẳng \(CH.\)
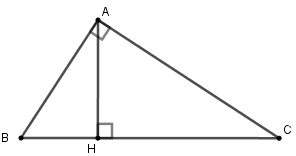
Ta có \(AB:AC = 3:7\) , đặt \(AB = 3a;AC = 7a\,\left( {a > 0} \right)\)
Theo hệ thức lượng \(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\)\( \Rightarrow \dfrac{1}{{{{42}^2}}} = \dfrac{1}{{9{a^2}}} + \dfrac{1}{{49{a^2}}} \Rightarrow \dfrac{1}{{1764}} = \dfrac{{58}}{{441{a^2}}}\)
\( \Rightarrow 441{a^2} = 102312 \Rightarrow a = 2\sqrt {58} \) (TM )
\( \Rightarrow AB = 6\sqrt {58} ;AC = 14\sqrt {58} \)
Theo định lý Pytago cho tam giác vuông \(AHC\) ta có \(CH = \sqrt {A{C^2} - A{H^2}} = \sqrt {{{\left( {14\sqrt {58} } \right)}^2} - {{42}^2}} = 98\)
Vậy \(CH = 98\).
Tính \(x,y\) trong hình vẽ sau:
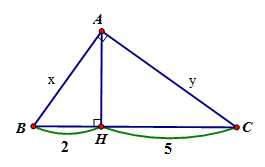
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
\(A{H^2} = BH.CH\) \( \Rightarrow A{H^2} = 2.5 \Rightarrow AH = \sqrt {10} \)
Áp dụng định lý Pytago cho tam giác vuông \(AHB;AHC\) ta có
\(AB = \sqrt {A{H^2} + H{B^2}} = \sqrt {10 + 4} = \sqrt {14} ;\)\(AC = \sqrt {A{H^2} + H{C^2}} = \sqrt {10 + 25} = \sqrt {35} \)
Vậy \(x = \sqrt {14} ;y = \sqrt {35} \).
Tính \(x\) trong hình vẽ sau:
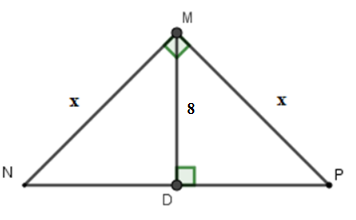
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
\(\dfrac{1}{{M{D^2}}} = \dfrac{1}{{M{N^2}}} + \dfrac{1}{{M{P^2}}}\) \( \Rightarrow \dfrac{1}{{64}} = \dfrac{1}{{{x^2}}} + \dfrac{1}{{{x^2}}} \Leftrightarrow \dfrac{1}{{64}} = \dfrac{2}{{{x^2}}} \Rightarrow {x^2} = 128 \Leftrightarrow x = 8\sqrt 2 \)
Vậy \(x = 8\sqrt 2 \).
Cho ABCD là hình thang vuông tại \(A\) và \(D.\) Đường chéo \(BD\)vuông góc với \(BC.\) Biết \(AD = 10cm,DC = 20cm\) . Tính độ dài \(BC\).
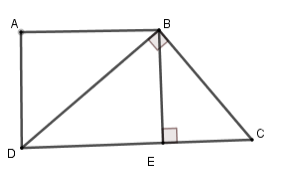
Kẻ \(BE \bot CD\) tại \(E\)
Suy ra tứ giác \(ABED\) là hình chữ nhật (vì \(\widehat A = \widehat D = \widehat E = 90^\circ \)) nên \(BE = AD = 10\,\,cm\)
Đặt \(EC = x\,\left( {0 < x < 25} \right)\) thì \(DE = 20 - x\)
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông \(BCD\) ta có
\(\begin{array}{l}B{E^2} = ED.EC \Leftrightarrow x\left( {20 - x} \right) = 100\\ \Leftrightarrow {x^2} - 20x + 100 = 0\\ \Leftrightarrow {\left( {x - 10} \right)^2} = 0 \Leftrightarrow x = 10\left( {tm} \right)\end{array}\)
Với \(EC = 10\), theo định lý Pytago ta có \(BC = \sqrt {B{E^2} + E{C^2}} = \sqrt {{{10}^2} + {{10}^2}} = 10\sqrt {2} \)
Vậy \(BC = 10\sqrt {2} \,cm\).

