Cho tam giác \(ABC\) vuông tại \(A\), \(AH \bot BC\)( \(H\) thuộc BC ). Cho biết \(AB:AC = 4:5\) và \(BC = \sqrt {41} cm.\) Tính độ dài đoạn thẳng \(CH\) (làm tròn đến chữ số thập phân thứ nhất).

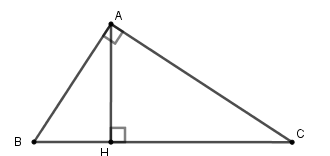
Ta có \(AB:AC = 4:5\)\( \Leftrightarrow \dfrac{{AB}}{4} = \dfrac{{AC}}{5} \Rightarrow \dfrac{{A{B^2}}}{{16}} = \dfrac{{A{C^2}}}{{25}} = \dfrac{{A{B^2} + A{C^2}}}{{16 + 25}} = \dfrac{{41}}{{41}} = 1\)

(Vì theo định lý Pytago ta có \(A{B^2} + A{C^2} = B{C^2} \Leftrightarrow A{B^2} + A{C^2} = {\left( {\sqrt {41} } \right)^2} = 41)\)

Nên  \(\dfrac{{A{B^2}}}{{16}} = 1 \Rightarrow A{B^2} = 16 \Rightarrow AB = 4\); \(\dfrac{{A{C^2}}}{{25}} = 1 \Rightarrow AC = 5\)

Theo hệ thức lượng trong tam giác vuông \(ABC\) ta có \(A{C^2} = CH.BC \Rightarrow CH = \dfrac{{A{C^2}}}{{BC}} = \dfrac{{25}}{{\sqrt {41} }} \approx 3,9\)

Vậy \(CH \approx 3,9\).