Câu hỏi:
2 năm trước
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH.$ Cho biết $AB:AC = 3:4$ và $AH = 6cm.$ Tính độ dài các đoạn thẳng $CH.$
Trả lời bởi giáo viên
Đáp án đúng: a
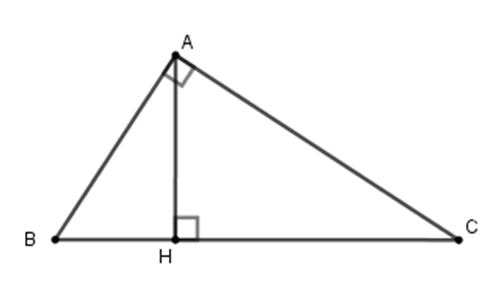
Ta có $AB:AC = 3:4$ , đặt $AB = 3a;AC = 4a\,\left( {a > 0} \right)$
Theo hệ thức lượng $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$$ \Rightarrow \dfrac{1}{{36}} = \dfrac{1}{{9{a^2}}} + \dfrac{1}{{16{a^2}}} \Rightarrow \dfrac{1}{{36}} = \dfrac{{25}}{{144{a^2}}} \Rightarrow a = \dfrac{5}{2}$ (TM )
$ \Rightarrow AB = 7,5;AC = 10$
Theo định lý Pytago cho tam giác vuông $AHC$ ta có $CH = \sqrt {A{C^2} - A{H^2}} = \sqrt {100 - 36} = 8$
Vậy $CH = 8$.
Hướng dẫn giải:
Bước 1: Tính $AB,AC$ dựa vào tỉ lệ cho trước và hệ thức $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$
Bước 2: Tính $CH$ theo định lý Pytago
Câu hỏi khác
- Bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông toán 9 có lời giải
- Bài tập một số hệ thức về cạnh và góc trong tam giác vuông toán 9 có lời giải
- Bài tập tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập ứng dụng thực tế tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập hay và khó chương hệ thức lượng trong tam giác vuông toán 9 có lời giải
