Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Biết \(AB:AC = 3:4\) và \(AB + AC = 21cm\).
Tính độ dài các đoạn \(AH,BH,CH\).
Trả lời bởi giáo viên
Đáp án đúng: d
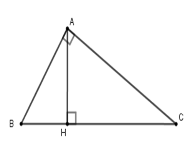
Ta có $AB = 9;AC = 12;BC = 15$
$ \Rightarrow AH.BC = AB.AC \Rightarrow AH = \dfrac{{AB.AC}}{{BC}}$$ = \dfrac{{12.9}}{{15}} = 7,2$ $A{B^2} = BH.BC \Rightarrow BH $$= \dfrac{{A{B^2}}}{{BC}} $$= \dfrac{{81}}{{15}} = 5,4$
$ \Rightarrow CH = BC - BH = 15 - 5,4 = 9,6$
Vậy $AH = 7,2;BH = 5,4;CH = 9,6$.
Hướng dẫn giải:
Sử dụng các hệ thức giữa cạnh và đường cao trong tam giác vuông: \(A{B^2} = BH.BC\) và $AH.BC = AB.AC$
Câu hỏi khác
- Bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông toán 9 có lời giải
- Bài tập một số hệ thức về cạnh và góc trong tam giác vuông toán 9 có lời giải
- Bài tập tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập ứng dụng thực tế tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập hay và khó chương hệ thức lượng trong tam giác vuông toán 9 có lời giải
