Trong dao động điều hòa
Ta có: .
$\begin{gathered}x = Acos(\omega t + \varphi ) \hfill \\v = x' = - \omega A\sin (\omega t + \varphi ) = \omega Acos(\omega t + \varphi + \frac{\pi }{2}) \hfill \\\end{gathered} $
Trong dao động điều hoà
Ta có:
$\begin{gathered}x = A\cos (\omega t + \varphi ) \hfill \\a = v' = - {\omega ^2}A\cos (\omega t + \varphi ) = - {\omega ^2}x ={\omega ^2}A\cos (\omega t + \varphi + \pi ) \hfill \\\end{gathered} $
Trong dao động điều hoà
$\begin{gathered}x = Acos(\omega t + \varphi ) \hfill \\v = x' = - \omega A\sin (\omega t + \varphi ) = \omega Acos(\omega t + \varphi + \frac{\pi }{2}) \hfill \\a = v' = - {\omega ^2}A\cos (\omega t + \varphi ) = - {\omega ^2}x = {\omega ^2}A\cos (\omega t + \varphi + \pi ) \hfill \\\end{gathered} $
Chọn câu đúng? Gia tốc trong dao động điều hòa
Ta có:
$\begin{gathered}x = Acos(\omega t + \varphi ) \hfill \\v = x' = - \omega A\sin (\omega t + \varphi ) = \omega Acos(\omega t + \varphi + \frac{\pi }{2}) \hfill \\a = v' = - {\omega ^2}A\cos (\omega t + \varphi ) = - {\omega ^2}x = {\omega ^2}A\cos (\omega t + \varphi + \pi ) \hfill \\\end{gathered} $
Mặt khác: gia tốc $a$ luôn hướng về vị trí cân bằng
Gia tốc: $a = - {\omega ^2}x$
$x=0=>a=0$
Một vật đang dao động điều hoà, khi vật chuyển động từ vị trí biên về vị trí cân bằng thì
Khi vật chuyển động từ vị trí biên về vị trí cân bằng, ta có:
+ vận tốc tăng
+ li độ giảm
=> Vật chuyển động nhanh dần, gia tốc có độ lớn giảm dần
Mặt khác: gia tốc luôn hướng về vị trí cân bằng
Khi một vật dao động điều hòa, chuyển động của vật từ vị trí biên về vị trí cân bằng là chuyển động:
Khi vật từ vị trí biên về vị trí cân bằng:
+ vận tốc tăng
+ li độ giảm
=> Vật chuyển động nhanh dần
Khi nói về dao động điều hoà của một vật, phát biểu nào sau đây sai?
Ta có: gia tốc a
+ Gia tốc luôn hướng về vị trí cân bằng
+ a=-ω2x
Vận tốc: trong 1 chu kì đổi chiều 2 lần
Tại thời điểm t thì tích của li độ và vận tốc của vật dao động điều hòa âm (x.v < 0), khi đó
Ta có: x.v < 0, có thể xảy ra 2 TH
+ x > 0,v < 0 : Vật đi từ A => 0: Vật đang chuyển động danh dần theo chiều âm
+ x < 0, v > 0: Vật đi từ -A=> 0: Vật đang chuyển động nhanh dần theo chiều dương
=> x.v <0: Vật đang chuyển động nhanh dần về vị trí cân bằng
Đối với dao động cơ điều hòa, chu kì dao động là quãng thời gian ngắn nhất để một trạng thái của dao động lặp lại như cũ. Trạng thái cũ ở đây bao gồm những thông số nào?
Trạng thái của dao động bao gồm vị trí cũ và vận tốc cũ
Đồ thị biểu diễn mối quan hệ giữa li độ và thời gian là một:
Đồ thị của dao động điều hòa là một đường hình sin
=> Chọn D
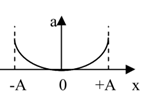
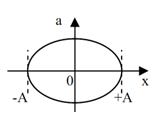
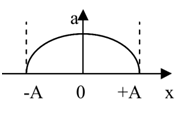
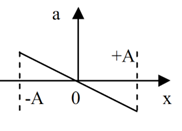
Đồ thị nào sau đây thể hiện đúng sự biến thiên của gia tốc a theo li độ x của một vật dao động điều hoà với biên độ (A)
Ta có: $a = - {\omega ^2}x$
=> (có dạng đồ thị của hàm số y=ax) Đồ thị (a-x) là đoạn thẳng đi qua gốc tọa độ.
Chọn phát biểu đúng nhất? Hình chiếu của một chuyển động tròn đều lên một đường kính:
Hình chiếu của một chuyển động tròn đều lên một đường kính được xem là một dao động điều hòa
Chọn phát biểu sai về quan hệ giữa chuyển động tròn đều và dao động điều hoà là hình chiếu của nó.
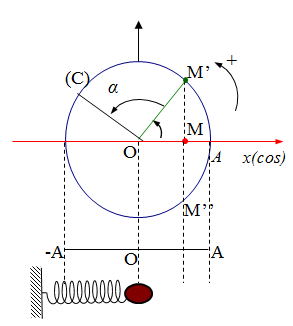
DĐĐH được xem là hình chiếu của một chất điểm chuyển động tròn đều lên một trục nằm trong mặt phẳng quỹ đạo. Với: \(A = R;\omega = \frac{v}{R}\)
Vật có đồ thị li độ dao động như hình vẽ. Biên độ và chu kì của vật là:
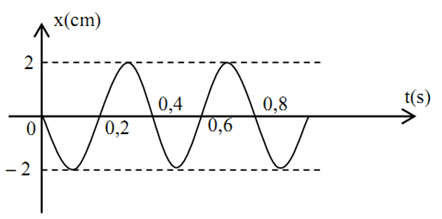
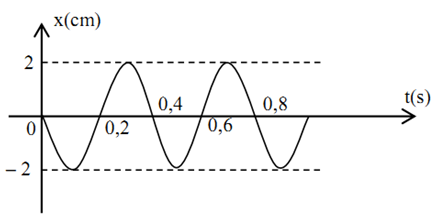
Từ đồ thị, ta có:
$\begin{gathered}A = 2cm \hfill \\T = 0,4{\text{s}} \hfill \\\end{gathered} $
Vật có đồ thị dao động như hình vẽ. Vận tốc cực đại có giá trị
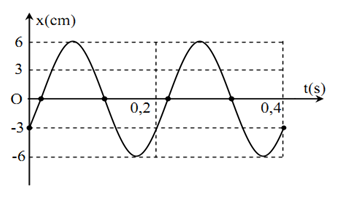
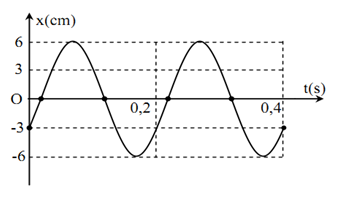
Ta có:
$\begin{gathered}A = 6cm \hfill \\2T = 0,4{\text{s}} \to T = 0,2{\text{s}} \to \omega {\text{ = }}\frac{{2\pi }}{T} = 10\pi ra{\text{d}}/s \hfill \\\end{gathered} $
$ \to {v_{{\text{max}}}} = A\omega = 60\pi cm/s$
Vật dao động điều hòa có đồ thị vận tốc - thời gian như hình vẽ. Tần số góc và pha ban đầu của li độ của vật là:
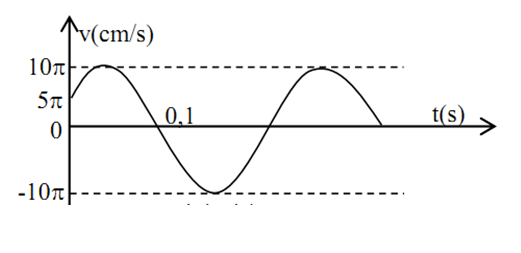
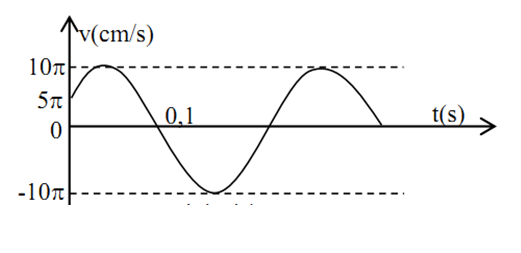
Ta có:
$\left\{ \begin{gathered}A\omega = 10\pi cm/s \hfill \\\dfrac{{5T}}{{12}} = 0,1{\text{s}} \to T = 0,24{\text{s}} \to \omega = \dfrac{{25\pi }}{3}ra{\text{d}}/s \hfill \\\end{gathered} \right.$
Tại \(t = 0\): \(\left\{ \begin{array}{l}v = 5\pi \\v > 0\end{array} \right. \leftrightarrow \left\{ \begin{array}{l} - A\omega \sin \varphi {\rm{ = 5}}\pi \\{\rm{sin}}\varphi < 0\end{array} \right. \leftrightarrow \left\{ \begin{array}{l}\sin \varphi {\rm{ = }}\dfrac{{{\rm{ - 5}}\pi }}{{10\pi }} = \dfrac{{{\rm{ - 1}}}}{2}\\{\rm{sin}}\varphi < 0\end{array} \right. \to \varphi = \left[ \begin{array}{l} - \dfrac{\pi }{6}\\\dfrac{{7\pi }}{6}\end{array} \right.\)
Mặt khác, vận tốc đang tăng => \(\varphi = \dfrac{{7\pi }}{6}\)
Vật dao động điều hòa hàm cosin có gia tốc biểu diễn như hình. Biên độ và pha ban đầu của vật là:
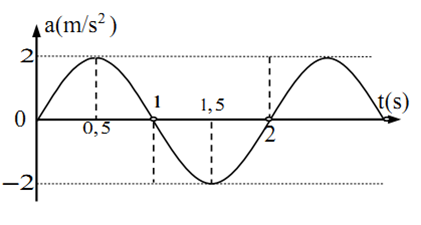
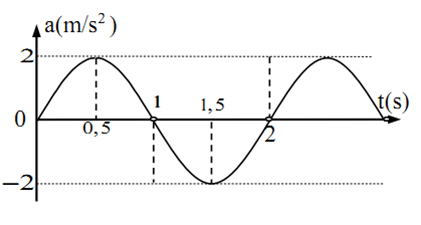
Ta có:
$\left\{ \begin{gathered}A{\omega ^2} = 2m/{s^2} \hfill \\T = 2{\text{s}} \to \omega = \pi ra{\text{d}}/s \hfill \\\end{gathered} \right. \to A = \frac{2}{{{\pi ^2}}} = 0,2m = 20cm$
Tại t=0: a=0 và đang đi lên => x=0 và đi theo chiều âm.
$\to \left\{ \begin{gathered}x = 0 \hfill \\v < 0 \hfill \\\end{gathered} \right. \leftrightarrow \left\{ \begin{gathered}Ac{\text{os}}\varphi {\text{ = 0}} \hfill \\{\text{sin}}\varphi > 0 \hfill \\\end{gathered} \right. \leftrightarrow \left\{ \begin{gathered}c{\text{os}}\varphi {\text{ = 0}} \hfill \\{\text{sin}}\varphi > 0 \hfill \\\end{gathered} \right. \to \varphi = \frac{\pi }{2}$
$ \to A = 20cm,\varphi = \frac{\pi }{2}$
a
a
Một vật dao động điều hòa với phương trình $x = Acos\left( {\omega t + \varphi } \right)$. \(\varphi \) được gọi là:
Ta có: \(x = Acos\left( {\omega t + \varphi } \right)\)
+ \(x\): li độ dao động của vật
+ \(A\): Biên độ dao động của vật
+ \(\omega \): Tần số góc của dao động
+ \(\varphi \): Pha ban đầu của dao động
+ \(\omega t + \varphi \): Pha dao động tại thời điểm t
s
s