Cho hình lăng trụ đứng \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\) có đáy $A B C$ là tam giác cân tại \(C,AB = \) \(A{A^\prime } = a\). Góc giữa đường thẳng \(B{C^\prime }\) và mặt phẳng \(\left( {AB{B^\prime }{A^\prime }} \right)\) bằng \({60^0}\). Gọi $M, N, P$ lần lượt là trung điểm của đoạn \(B{B^\prime },C{C^\prime }\) và $B C$. Tính khoảng cách giữa $A M$ và $N P$.
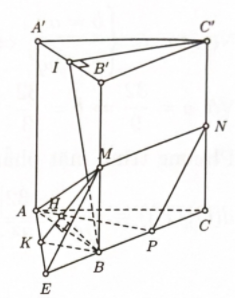
Bước 1: Gọi \(I\) là trung điểm \({A^\prime }{B^\prime }\). Tính BI, BC
Gọi \(I\) là trung điểm \({A^\prime }{B^\prime }\)\( \Rightarrow {C^\prime }I \bot {A^\prime }{B^\prime } \Rightarrow {C^\prime }I \bot \left( {AB{B^\prime }{A^\prime }} \right)\).
\(BI = \sqrt {B{B^{\prime 2}} + {B^\prime }{I^2}} = \dfrac{{a\sqrt 5 }}{2} \cdot B{C^\prime }\)\( = \dfrac{{BI}}{{\cos \widehat {{C^\prime }BI}}} = a\sqrt 5 \)
\(BC = \sqrt {B{C^{\prime 2}} - C{C^{\prime 2}}} = 2a\).
Bước 2: Gọi \(E\) là điểm sao cho \(B\) là trung điểm $E P$. Chứng minh \(d(AM,NP)\)\( = 2d(B;(AME))\).
Gọi \(E\) là điểm sao cho \(B\) là trung điểm $E P$.
\( \Rightarrow MNPE\) là hình bình hành \( \Rightarrow EM//NP\)
\( \Rightarrow d(AM,NP) = d(P;(AME))\)\( = 2d(B;(AME))\).
Bước 3: Tính \(d(AM,NP)\)
Ké \(BK \bot AE(K \in AE),BH \bot MK(H \in KM)\)
\( \Rightarrow AE \bot \left( {BMK} \right) \Rightarrow AE \bot BH\)\( \Rightarrow BH \bot \left( {AME} \right)\)
\( \Rightarrow d(B,(AME)) = BH.\)
Tam giác $A P E$ có \(AB = BP = BE = a\)
\( \Rightarrow \Delta APE\) vuông ở \(A\)
\( \Rightarrow BK//AP\).
Mà \(B\) là trung điểm \(EP\)\( \Rightarrow KB = \dfrac{1}{2}AP\).
Ta có: \(A{P^2} = \dfrac{{A{B^2} + A{C^2}}}{2} - \dfrac{{B{C^2}}}{4}\)\( \Rightarrow AP = \dfrac{{a\sqrt 6 }}{2} \Rightarrow BK = \dfrac{{a\sqrt 6 }}{4}\).
\(BH = \dfrac{{BK.BM}}{{\sqrt {B{K^2} + B{M^2}} }} = \dfrac{{a\sqrt {15} }}{{10}}\)\( \Rightarrow d(AM,NP) = \dfrac{{a\sqrt {15} }}{5}\)
Cho tứ diện đều $A B C D$ có cạnh bằng \(\sqrt {11} \). Gọi \(I\) là trung điểm cạnh $C D$. Tính khoảng cách giữa hai đường thẳng $A C$ và $B I$.
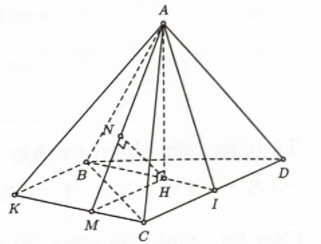
Bước 1: Dựng hình bình hành \(BICK\). Gọi \(H\) là tâm \(\Delta BCD\). Vẽ \(HM \bot KC\) tại \(M,HN \bot AM\) tại \(N\).
Dựng hình bình hành \(BICK\)
\( \Rightarrow BICK\) là hình chữ nhật do \(BI \bot CD\).
Gọi \(H\) là tâm \(\Delta BCD\).
Vẽ \(HM \bot KC\) tại \(M,HN \bot AM\) tại \(N\).
Bước 2: Chứng minh \(d(AC,BI) = HN\)
Ta có \(CK \bot (AHM) \Rightarrow CK \bot HN\)\( \Rightarrow HN \bot (ACK)\).
Ta có \(BI//(ACK)\)
\( \Rightarrow d(AC,BI) = d(BI,(ACK))\)\( = d(H,(ACK)) = HN.\)
Bước 3: Tính HN
Xét tam giác vuông \(ABH\) có \(AH = \sqrt {A{B^2} - B{H^2}} \)\( = \sqrt {11 - {{\left( {\dfrac{{\sqrt {11} \cdot \sqrt 3 }}{3}} \right)}^2}} = \dfrac{{\sqrt {66} }}{3}\)
Ta có \(HM = CI = \dfrac{{\sqrt {11} }}{2}\) (vì $B I C K$ là hình chữ nhật)
Xét \(\Delta AHM\) vuông có \(HN = \dfrac{{AH.HM}}{{\sqrt {A{H^2} + H{M^2}} }} = \dfrac{{\dfrac{{\sqrt {66} }}{3} \cdot \dfrac{{\sqrt {11} }}{2}}}{{\sqrt {\dfrac{{22}}{3} + \dfrac{{11}}{4}} }}\)\( = \sqrt 2 \)\( \Rightarrow d(AC,BI) = \sqrt 2 \).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a tâm O, \(SA \bot \left( {ABCD} \right)\) và \(SA = a\sqrt 6 \). Tính khoảng cách giữa hai đường thẳng SO và BC.
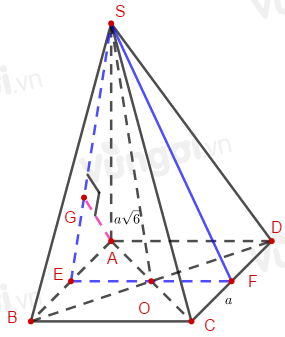
Bước 1:
Gọi E, F lần lượt là trung điểm của AB và CD.
=> EF//BC
=> BC//(SEF)
Bước 2:
Mà \(O \in EF\)\( \Rightarrow SO \subset \left( {SEF} \right)\)
\(\begin{array}{l} \Rightarrow d\left( {BC,SO} \right) = d\left( {BC,\left( {SEF} \right)} \right)\\ = d\left( {B,\left( {SEF} \right)} \right) = d\left( {A,\left( {SEF} \right)} \right)\end{array}\)
Bước 3:
Kẻ AG vuông góc với SE.
Ta có \(EF\parallel AD,AD \bot AB \Rightarrow EF \bot AB\)
Mà \(EF \bot SA\)
\(\begin{array}{l}\left. \begin{array}{l} \Rightarrow EF \bot \left( {SAB} \right) \Rightarrow \left( {SEF} \right) \bot \left( {SAB} \right)\\\left( {SEF} \right) \cap \left( {SAB} \right) = SE\\AG \subset \left( {SAB} \right),AG \bot SE\end{array} \right\}\\ \Rightarrow AG \bot \left( {SEF} \right)\\ = > d\left( {A,\left( {SEF} \right)} \right) = AG\end{array}\)
Bước 4:
Ta có \(AE = \dfrac{{AB}}{2} = \dfrac{a}{2};SA = a\sqrt 6 \).
\(\begin{array}{l}\dfrac{1}{{A{G^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{E^2}}} = \dfrac{1}{{6{a^2}}} + \dfrac{4}{{{a^2}}} = \dfrac{{25}}{{6{a^2}}}\\ = > d\left( {BC,SO} \right) = AG = \dfrac{{a\sqrt 6 }}{5}\end{array}\)
Cho hình chóp $S . A B C$ có đáy $A B C$ là tam giác vuông cân tại \(A,AB = a\), $S A$ vuông góc với mặt phẳng đáy và \(SA = \sqrt 3 a\). Gọi \(M\) là trung điểm $B C$. Khoảng cách giữa hai đường thẳng $A C$ và $S M$ bằng
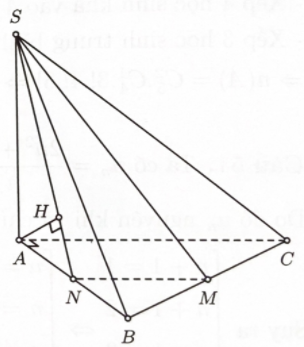
Gọi \(N\) là trung điểm $A B$. Kẻ \(AH \bot SN\).
Vì \(MN//AC,MN \subset (SMN)\) nên \(AC//(SMN)\)
\( \Rightarrow d(SM;AC) = d(AC;(SMN))\)\( = d(A;(SMN))\)
Ta có \(\left\{ {\begin{array}{*{20}{l}}{MN \bot AB}\\{MN \bot SA}\end{array}} \right.\)\( \Rightarrow MN \bot (SAB) \Rightarrow MN \bot AH\).
Từ đó suy ra \(AH \bot (SMN)\)\( \Rightarrow d(SM;AC) = AH\).
Lại có \(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{S^2}}} + \dfrac{1}{{A{N^2}}} = \dfrac{{13}}{{3{a^2}}}\)\( \Rightarrow AH = \dfrac{{\sqrt {39} a}}{{13}}\).
Cho tứ diện ABCD có \(\widehat {ABC} = \widehat {ADC} = \widehat {BCD} = {90^0 },BC = 2a,CD = a\), góc giữa đường thẳng AB và mặt phẳng \((BCD)\) bằng \({60^0}\). Tính khoảng cách giữa hai đường thẳng AC và BD.
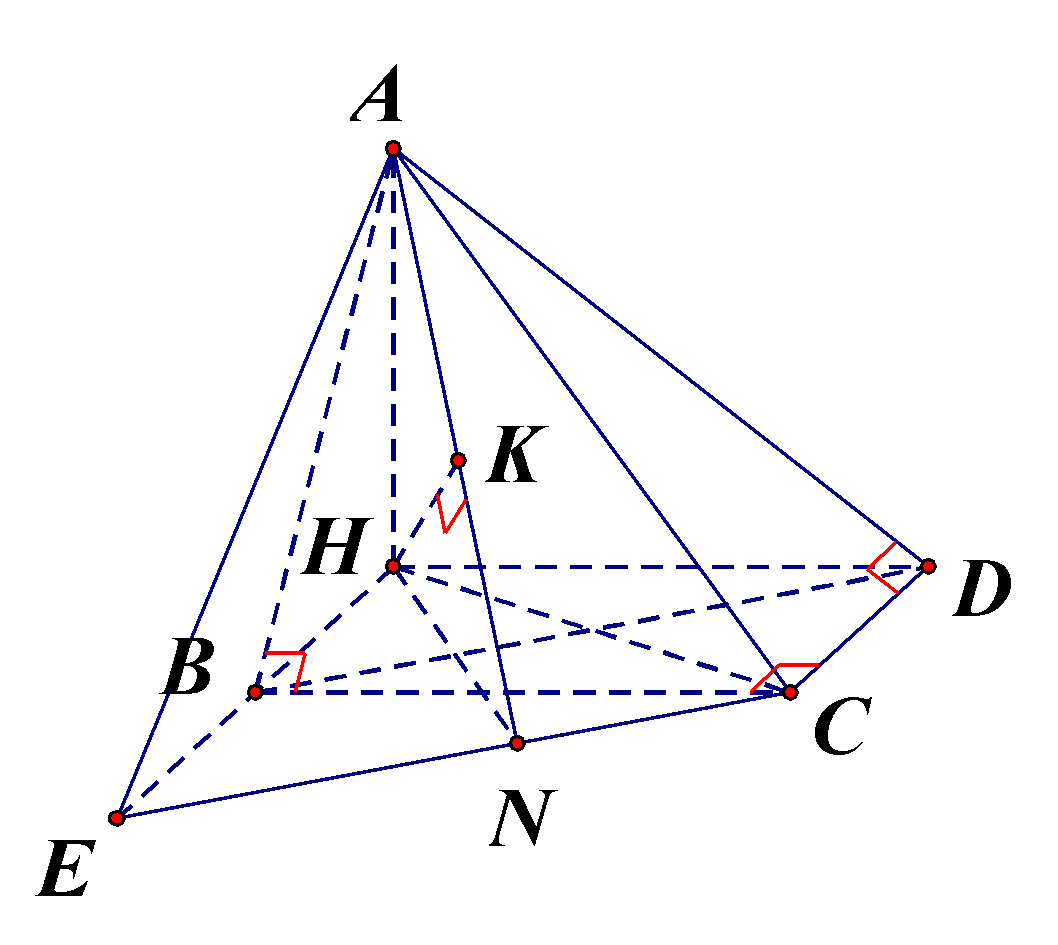
Bước 1: Gọi \(H\) là hình chiếu vuông góc của \(A\) lên mặt phẳng \((BCD)\). Chứng minh HBCD là hình chữ nhật và tìm các cạnh của tứ giác.
Gọi \(H\) là hình chiếu vuông góc của \(A\) lên mặt phẳng \((BCD)\).
\({\rm{ Do }}\left\{ {\begin{array}{*{20}{l}}{BC \bot AB}\\{BC \bot AH,({\rm{ do }}AH \bot (BCD))}\end{array}} \right.\)
\( \Rightarrow BC \bot (ABH) \Rightarrow BC \bot BH(1)\)
Tương tự \(\left\{ {\begin{array}{*{20}{l}}{CD \bot AD}\\{CD \bot AH,({\rm{ do }}AH \bot (BCD))}\end{array}} \right.\)
\( \Rightarrow CD \bot (ADH) \Rightarrow CD \bot DH(2)\)
Ta có \(\widehat {BCD} = {90^0 }\). (3)
Từ (1), (2), (3) nên tứ giác HBCD là hình chữ nhật có \(BC = HD = 2a;HB = DC = a\) và \((\widehat {AB,(BCD)}) = \overline {(AB,BH)} = \widehat {ABH} = {60^0}\).
Bước 2: Gọi \(E\) là đỉnh của hình bình hành BDCE. HN là đường cao tam giác HEC. Chứng minh \(d(AC,BD) = \dfrac{1}{2}HK\)
Gọi \(E\) là đỉnh của hình bình hành BDCE.
Khoảng cách giữa hai đường thẳng AC và BD bằng
\(d(AC,BD) = d(BD,(AEC))\)\( = d(B,(AEC)) = \dfrac{1}{2}d(H,(AEC))\).
Gọi HN là đường cao tam giác HEC, đường thẳng HK là đường cao tam giác AHN.
Ta có \(\left\{ {\begin{array}{*{20}{l}}{CE \bot HN}\\{CE \bot AH,({\rm{ do }}AH \bot (BCD))}\end{array}} \right.\)
\( \Rightarrow CE \bot (AHN) \Rightarrow CE \bot HK\) và \(AN \bot HK\) nên \(HK \bot (AEC)\).
Vậy \(d(AC,BD) = \dfrac{1}{2}d(H,(AEC)) = \dfrac{1}{2}HK\).
Bước 3: Tính \(d(AC,BD)\)
Trong \(\Delta HEC\) có \(HE.BC = EC.HN\)\( \Rightarrow HN = \dfrac{{HE.BC}}{{EC}} = \dfrac{{4a}}{{\sqrt 5 }}\).
Trong \(\Delta AHN\) có \(\dfrac{1}{{H{K^2}}} = \dfrac{1}{{H{A^2}}} + \dfrac{1}{{H{N^2}}}\)\( = \dfrac{1}{{3{a^2}}} + \dfrac{5}{{16{a^2}}} = \dfrac{{31}}{{48{a^2}}}\)\( \Rightarrow HK = \dfrac{{4\sqrt 3 a}}{{\sqrt {31} }}\)
Vậy \(d(AC,BD) = \dfrac{1}{2}HK = \dfrac{{2\sqrt 3 a}}{{\sqrt {31} }}\).
Cho hình hộp chữ nhật \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có \(AB = a,AD = 2a,A{A^\prime } = a\). Gọi \(M\) là điểm trên đoạn $A D$ với \(\dfrac{{AM}}{{MD}} = 3\). Gọi \(x\) là độ dài khoảng cách giữa hai đường thẳng \(A{D^\prime },{B^\prime }C\) và \(y\) là độ dài khoảng cách từ \(M\) đến mặt phẳng \(\left( {A{B^\prime }C} \right)\). Tính giá trị $x y$.
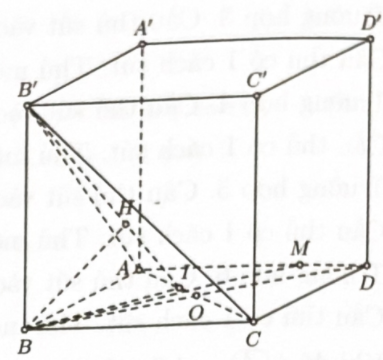
Bước 1: \(d\left( {M,\left( {A{B^\prime }C} \right)} \right) = \dfrac{3}{4}d\left( {B;\left( {A{B^\prime }C} \right)} \right)\)
Ta có \({B^\prime }C//{A^\prime }D \Rightarrow {B^\prime }C//\left( {AD{D^\prime }{A^\prime }} \right) \supset A{D^\prime }\)
\( \Rightarrow d\left( {{B^\prime }C,A{D^\prime }} \right) = d\left( {C,\left( {AD{D^\prime }{A^\prime }} \right)} \right) = CD = a.\)
Suy ra \(x = a\). Lại có \(\dfrac{{MA}}{{DA}} = \dfrac{3}{4}\) .
\( \Rightarrow d\left( {M,\left( {A{B^\prime }C} \right)} \right) = \dfrac{3}{4}d\left( {D,\left( {A{B^\prime }C} \right)} \right) = \dfrac{3}{4}d\left( {B;\left( {A{B^\prime }C} \right)} \right)\).
Bước 2: Gọi I là hình chiếu vuông góc của \(B\) lên $A C$
Gọi I là hình chiếu vuông góc của \(B\) lên $A C$ ta có: \(\left\{ {\begin{array}{*{20}{l}}{AC \bot BI}\\{AC \bot B{B^\prime }}\end{array} \Rightarrow AC \bot \left( {B{B^\prime }I} \right)} \right.\)
Bước 3: Gọi \(H\) là hình chiếu của \(B\) lên \({B^\prime }I\)
Gọi \(H\) là hình chiếu của \(B\) lên \({B^\prime }I\) ta có: \(\left\{ {\begin{array}{*{20}{l}}{BH \bot {B^\prime }I}\\{BH \bot AC}\end{array} \Rightarrow BH \bot \left( {{B^\prime }AC} \right) \Rightarrow d\left( {B,\left( {A{B^\prime }C} \right)} \right) = BH.} \right.\) Trong tam giác $A B C$, ta có: \(AB \cdot BC = AC \cdot BI \Rightarrow BI = \dfrac{{AB \cdot BC}}{{AC}} = \dfrac{{a \cdot 2a}}{{a\sqrt 5 }} = \dfrac{{2a\sqrt 5 }}{5}\). Trong tam giác \(B{B^\prime }I\), ta có: \(\dfrac{1}{{B{H^2}}} = \dfrac{1}{{B{I^2}}} + \dfrac{1}{{B{B^{\prime 2}}}} \Rightarrow BH = \dfrac{{BI \cdot B{B^\prime }}}{{\sqrt {B{I^2} + B{B^{\prime 2}}} }} = \dfrac{{2a}}{3}\) \( \Rightarrow d\left( {M,\left( {A{B^\prime }C} \right)} \right) = \dfrac{3}{4} \cdot \dfrac{{2a}}{3} = \dfrac{a}{2}.\) Suy ra \(y = \dfrac{a}{2}.\) Vậy \(xy = \dfrac{{{a^2}}}{2}\).
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật, biết \(AB = 2a,\,\,AD = a,\,\,SA = 3a\) và \(SA\) vuông góc với mặt phẳng đáy. Gọi \(M\) là trung điểm cạnh \(CD\). Khoảng cách giữa hai đường thẳng \(SC\) và \(BM\) bằng:
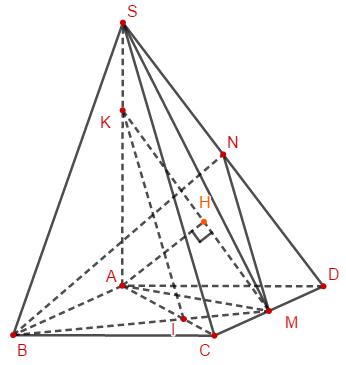
Gọi I là giao điểm của MB và AC, kẻ \(IK//SC\left( {K \in SA} \right)\), kẻ \(MN//SC\left( {N \in S{\rm{D}}} \right)\). Khi đó \(KI,MN \subset \left( {BMN} \right)\). Kẻ \(AH \bot KM\)
Do ABCD là hình chữ nhật có AB=2CD nên \(AM \bot BM \Rightarrow BM \bot \left( {SAM} \right)\)
\( \Rightarrow \left( {BMN} \right) \bot \left( {SAM} \right) \Rightarrow AH \bot \left( {BMN} \right)\)
Ta có AI=2CI (vì CM//AB và AB=2CM)
Suy ra AK=2KS và
\(\begin{array}{l}d\left( {SC,BM} \right) = d\left( {SC,\left( {BMN} \right)} \right) = d\left( {C,\left( {BMN} \right)} \right)\\ = \dfrac{1}{2}d\left( {A,\left( {BMN} \right)} \right) = \dfrac{1}{2}AH\end{array}\)
\(\begin{array}{l}AK = \dfrac{2}{3}SA = 2{\rm{a}};AM = AD\sqrt 2 = a\sqrt 2 \\ \Rightarrow \dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{K^2}}} + \dfrac{1}{{A{M^2}}} = \dfrac{1}{{4{{\rm{a}}^2}}} + \dfrac{1}{{2{{\rm{a}}^2}}} = \dfrac{3}{{4{{\rm{a}}^2}}}\\ \Rightarrow AH = \dfrac{{2a\sqrt 3 }}{3}\end{array}\)
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), cạnh bên \(SD = \dfrac{{a\sqrt {17} }}{2}\). Hình chiếu vuông góc của \(S\) lên mặt phẳng \(\left( {ABCD} \right)\) là trung điểm \(H\) của đoạn thẳng \(AB\). Gọi \(E\) là trung điểm của \(AD\). Tính khoảng cách giữa hai đường thẳng \(HE\) và \(SB\).
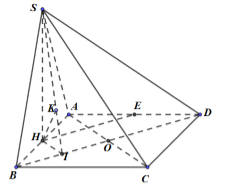
Ta có: \(HE//\left( {SBD} \right) \Rightarrow d\left( {HE;SB} \right) = d\left( {HE;\left( {SBD} \right)} \right) = d\left( {H;\left( {SBD} \right)} \right)\)
Gọi O là tâm của hình vuông, I là trung điểm của BO.
\( \Rightarrow HI//AC\), mà \(BD \bot AC \Rightarrow HI \bot BD\)
Mà \(SH \bot BD \Rightarrow BD \bot \left( {SHI} \right) \Rightarrow BD \bot HK\) \(\left( {K \in SI,\,\,HK \bot SI} \right)\)
\( \Rightarrow d\left( {H;\left( {SBD} \right)} \right) = HK\)
\(HD = \sqrt {{a^2} + \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 5 }}{2},\,\,SH = \sqrt {S{D^2} - H{D^2}} = \sqrt {\dfrac{{17{a^2}}}{4} - \dfrac{{5{a^2}}}{4}} = a\sqrt 3 \)
\(HI = \dfrac{1}{2}AO = \dfrac{1}{2}.\dfrac{{a\sqrt 2 }}{2} = \dfrac{{a\sqrt 2 }}{4}\)
\(\dfrac{1}{{H{K^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{I^2}}} \Leftrightarrow \dfrac{1}{{H{K^2}}} = \dfrac{1}{{3{a^2}}} + \dfrac{8}{{{a^2}}} = \dfrac{{25}}{{3{a^2}}} \Rightarrow HK = \dfrac{{a\sqrt 3 }}{5}\)
Vậy \(d\left( {HE;SB} \right) = \dfrac{{a\sqrt 3 }}{5}.\)
Trong các mệnh đề sau, mệnh đề nào đúng?
Đáp án A: Đúng
Đáp án B: Sai, do phát biểu này thiếu yếu tố "đường vuông góc chung phải cắt nhau với hai đường thẳng đã cho".
Đáp án C: Sai, vì "mặt phẳng đi qua đường thẳng này và vuông góc với đường thẳng kia" chưa chắc đã tồn tại.
Đáp án D: Sai, do phát biểu này thiếu yếu tố vuông góc.
Trong các mệnh đề sau, mệnh đề nào sai?
Khoảng cách giữa hai đường thẳng chéo nhau $a$ và $b$ là khoảng cách từ một điểm $M$ thuộc đường thẳng $b$ đến mặt phẳng $(P)$ chứa $a$ và song song với $b$ chứ không phải khoảng cách giữa hai điểm như đáp án C nói nên C sai.
Cho hình chóp $S.ABCD $ có đáy $ABCD$ là hình vuông với \(AC = \dfrac{{a\sqrt 2 }}{2}\). Cạnh bên $SA$ vuông góc với đáy, $SB$ hợp với đáy góc \({60^0}\). Tính khoảng cách $d$ giữa hai đường thẳng $AD$ và $SC.$
Ta có \(SA \bot \left( {ABCD} \right) \Rightarrow \widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {\left( {SB;AB} \right)} = \widehat {SBA} = {60^0}\)
Tam giác $ABC$ vuông cân tại $B$ nên \(AB = BC = \dfrac{{AC}}{{\sqrt 2 }} = \dfrac{a}{2}\)
Xét tam giác vuông $SAB $ có : \(SA = AB.\tan {60^0} = \dfrac{a}{2}.\sqrt 3 = \dfrac{{a\sqrt 3 }}{2}\)
Ta có \(d\left( {AD;SC} \right) = d\left( {AD;\left( {SBC} \right)} \right) = d\left( {A;\left( {SBC} \right)} \right)\)
Kẻ \(AK \bot SB\).
Do \(\left\{ \begin{array}{l}BC \bot SA\\BC \bot AB\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AK\), mà \(AK \bot SB\) nên \(AK \bot \left( {SBC} \right)\)
Khi đó
\(d\left( {A;\left( {SBC} \right)} \right) = AK = \dfrac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \dfrac{{\dfrac{{a\sqrt 3 }}{2}.\dfrac{a}{2}}}{{\sqrt {{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\dfrac{a}{2}} \right)}^2}} }} = \dfrac{{a\sqrt 3 }}{4}\)
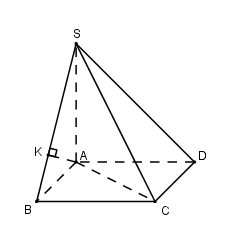
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O,$ cạnh bằng \(2\). Đường thẳng $SO$ vuông góc với mặt phẳng đáy $(ABCD)$ và $SO = \sqrt 3 $. Tính khoảng cách $d$ giữa hai đường thẳng $SA$ và $BD.$
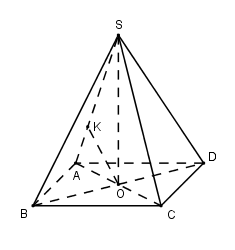
Ta có \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SO\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\).
Trong (SAC) kẻ \(OK \bot SA\,\,\left( 1 \right)\) ta có : \(OK \subset \left( {SAC} \right) \Rightarrow OK \bot BD\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta có $OK$ là đường vuông góc chung của $SA$ và $BD.$ Khi đó $d\left( {SA;BD} \right) = OK = \dfrac{{SO.OA}}{{\sqrt {S{O^2} + O{A^2}} }} = \dfrac{{\sqrt 3 .\dfrac{{2\sqrt 2 }}{2}}}{{\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{\left( {\dfrac{{2\sqrt 2 }}{2}} \right)}^2}} }} = \dfrac{{\sqrt {30} }}{5}.$
Cho hình lăng trụ $ABC.A’B’C’$ có đáy là tam giác đều cạnh có độ dài bằng $2a.$ Hình chiếu vuông góc của $A’$ lên mặt phẳng $(ABC)$ trùng với trung điểm $H$ của $BC.$ Tính khoảng cách $d$ giữa hai đường thẳng $BB’$ và $A’H.$
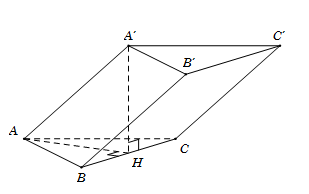
Do \(BB'\parallel AA'\) nên \(d\left( {BB';A'H} \right) = d\left( {BB';\left( {AA'H} \right)} \right) = d\left( {B;\left( {AA'H} \right)} \right).\)
Ta có \(\left\{ \begin{array}{l}BH \bot AH\\BH \bot A'H\end{array} \right. \Rightarrow BH \bot \left( {AA'H} \right)\)
Nên \(d\left( {B;\left( {AA'H} \right)} \right) = BH = \dfrac{{BC}}{2} = a.\)
Vậy khoảng cách \(d\left( {BB';A'H} \right) = a\).
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a.$ Cạnh bên $SA$ vuông góc với đáy. Biết rằng đường thẳng $SC$ tạo với đáy một góc ${60^0}.$ Khoảng cách giữa hai đường thẳng $AB$ và $SD$ là
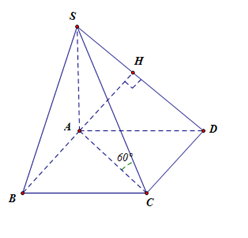
Ta có $AC = a\sqrt 2 .$ Do $SA \bot \left( {ABCD} \right)$ và $SC$ tạo với đáy góc ${60^0}$ nên $\widehat {SCA} = {60^0}$.
Khi đó $SA = AC\tan {60^0} = a\sqrt 6 $. Do $\left\{ \begin{array}{l}AB \bot AD\\AB \bot SA\end{array} \right. \Rightarrow AB \bot \left( {SAD} \right)$.
Trong (SAD) dựng $AH \bot SD\,\,\left( 1 \right)$ suy ra \(AB \bot AH\,\,\left( 2 \right)\) là đoạn vuông góc chung $AB$ và $SD$.
Ta có $AH = \dfrac{{SA.AD}}{{\sqrt {S{A^2} + A{D^2}} }} = \dfrac{{a\sqrt 6 .a}}{{\sqrt {6{a^2} + {a^2}} }} = \dfrac{{a\sqrt {42} }}{7}$
Vậy khoảng cách $d\left( {AB;SD} \right) = \dfrac{{a\sqrt {42} }}{7}.$
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cân tại $A,$ tam giác $SBC$ là tam giác đều cạnh $a$ và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng $SA$ và $BC.$
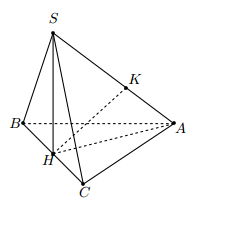
Gọi $H$ là trung điểm của $BC$ khi đó $SH \bot BC$.
Mặt khác $\left( {SBC} \right) \bot \left( {ABC} \right)$ do đó $SH \bot \left( {ABC} \right)$.
Ta có $SH = \dfrac{{a\sqrt 3 }}{2}$ và $AB = AC = \dfrac{a}{{\sqrt 2 }};AH = \dfrac{{BC}}{2} = \dfrac{a}{2}$.
Do $\left\{ \begin{array}{l}BC \bot AH\\BC \bot SH\end{array} \right. \Rightarrow BC \bot \left( {SHA} \right).$
Dựng $HK \bot SA$ khi đó $HK$ là đoạn vuông góc chung của $BC$ và $SA$.
Lại có $HK = \dfrac{{SH.AH}}{{\sqrt {S{H^2} + H{A^2}} }} = \dfrac{{a\sqrt 3 }}{4}$. Vậy $d\left( {SA;BC} \right) = \dfrac{{a\sqrt 3 }}{4}.$
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a,$ cạnh bên $SA$ vuông góc với mặt phẳng đáy. Biết mặt phẳng $(SBC)$ tạo với đáy một góc ${60^0}$ và $M$ là trung điểm của $SD.$ Tính khoảng cách $d$ giữa hai đường thẳng $AB$ và $CM.$
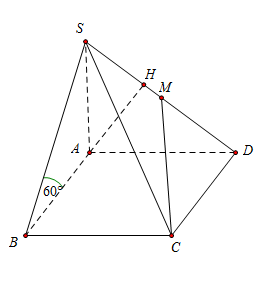
Ta có $\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) $
$\Rightarrow \widehat {SBA}$ là góc giữa $2$ mặt phẳng $\left( {SBC} \right)$ và $\left( {ABC} \right)$
Ta có $SA = AB\tan \widehat {SBA} = a\sqrt 3 $.
Do $AB||CD$ do đó $d\left( {AB;CM} \right) = d\left( {AB;\left( {CMD} \right)} \right) = d\left( {A;\left( {SCD} \right)} \right)$
Dựng \(AH \bot SD\,\,\,\left( 1 \right)\) ta có:
\(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\end{array} \right. \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot AH\,\,\left( 2 \right).\)
Từ (1) và (2) \( \Rightarrow AH \bot \left( {SCD} \right)\),
khi đó $d\left( {A;\left( {SCD} \right)} \right) = AH$
Lại có $AH = \dfrac{{SA.AD}}{{\sqrt {S{A^2} + A{D^2}} }}$
$= \dfrac{{a\sqrt 3 .a}}{{\sqrt {3{a^2} + {a^2}} }} = \dfrac{{a\sqrt 3 }}{2}.$
Do đó $d = \dfrac{{a\sqrt 3 }}{2}.$
Cho hình chóp $S.ABC$ có đáy $ABCD$ là hình vuông cạnh $a,$ tâm $O.$ Cạnh bên $SA = 2a$ và vuông góc với mặt đáy $(ABCD).$ Gọi $H$ và $K$ lần lượt là trung điểm của cạnh $BC$ và $CD.$ Tính khoảng cách giữa hai đường thẳng $HK$ và $SD.$
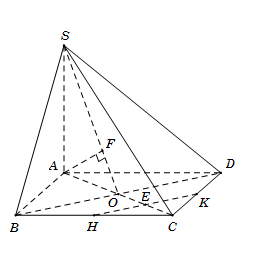
Gọi \(E = HK \cap AC.\) Do \(HK\parallel BD\) nên suy ra
\(d\left( {HK;SD} \right) = d\left( {HK;\left( {SBD} \right)} \right) = d\left( {E;\left( {SBD} \right)} \right) = \dfrac{1}{2}d\left( {A;\left( {SBD} \right)} \right)\) (vì $OE = \dfrac{1}{2}AO$)
Kẻ $AF \bot SO\,\,\left( 1 \right)$ ta có:
\(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot AF\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow AF \bot \left( {SBD} \right)\), khi đó
\(d\left( {A;\left( {SBD} \right)} \right) = AF = \dfrac{{SA.AO}}{{\sqrt {S{A^2} + A{O^2}} }} = \dfrac{{2a.\dfrac{{a\sqrt 2 }}{2}}}{{\sqrt {4{a^2} + \dfrac{{{a^2}}}{2}} }} = \dfrac{{2a}}{3}.\)
Vậy khoảng cách \(d\left( {HK;SD} \right) = \dfrac{1}{2}AF = \dfrac{a}{3}.\)
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O,$ cạnh bằng $4a.$ Cạnh bên $SA = 2a.$ Hình chiếu vuông góc của đỉnh $S$ trên mặt phẳng $(ABCD)$ là trung điểm của $H$ của đoạn thẳng $AO.$ Tính khoảng cách $d$ giữa các đường thẳng $SD$ và $AB.$
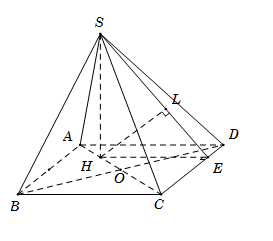
Do \(AB\parallel CD\) nên \(d\left( {SD;AB} \right) = d\left( {AB;\left( {SCD} \right)} \right) = d\left( {A;\left( {SCD} \right)} \right) = \dfrac{4}{3}d\left( {H;\left( {SCD} \right)} \right).\)
(Do \(AH \cap \left( {SCD} \right) = C \) \(\Rightarrow \dfrac{{d\left( {A;\left( {SCD} \right)} \right)}}{{d\left( {H;\left( {SCD} \right)} \right)}} = \dfrac{{AC}}{{HC}} = \dfrac{4}{3} \) \( \Rightarrow d\left( {A;\left( {SCD} \right)} \right) = \dfrac{4}{3}d\left( {H;\left( {SCD} \right)} \right)\))
Kẻ \(HE \bot CD\), kẻ \(HL \bot SE\,\,\left( 1 \right)\) ta có:
\(\left\{ \begin{array}{l}CD \bot SH\\CD \bot HE\end{array} \right. \Rightarrow CD \bot \left( {SHE} \right) \Rightarrow CD \bot HL\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow HL \bot \left( {SCD} \right)\)
\(\Rightarrow d\left( {H;\left( {SCD} \right)} \right) = HL\)
Tính được \(SH = \sqrt {S{A^2} - A{H^2}} = a\sqrt 2 \), \(HE = \dfrac{3}{4}AD = 3a.\)
Khi đó \(d\left( {H;\left( {SCD} \right)} \right) = HL = \dfrac{{SH.HE}}{{\sqrt {S{H^2} + H{E^2}} }} = \dfrac{{3a\sqrt 2 }}{{\sqrt {11} }}.\)
Vậy \(d\left( {SD;AB} \right) = \dfrac{4}{3}HL = \dfrac{{4a\sqrt {22} }}{{11}}.\)
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a,$ tam giác $SAD $ đều và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách $d$ giữa hai đường thẳng $SA$ và $BD.$
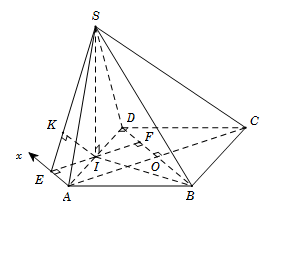
Gọi $I$ là trung điểm của $AD$ nên suy ra $SI \bot AD \Rightarrow SI \bot \left( {ABCD} \right)$ và \(SI = \dfrac{{a\sqrt 3 }}{2}\)
Kẻ \(Ax\parallel BD\). Do đó \(d\left( {BD;SA} \right) = d\left( {BD;\left( {SAx} \right)} \right) = d\left( {D;\left( {SAx} \right)} \right) = 2d\left( {I;\left( {SAx} \right)} \right)\)
(vì \(DI \cap \left( {SAx} \right) = A\) và \(IA = \dfrac{1}{2}DA\))
Kẻ \(IE \bot Ax\), kẻ \(IK \bot SE\,\,\left( 1 \right)\) ta có:
\(\left\{ \begin{array}{l}Ax \bot SI\\Ax \bot IE\end{array} \right. \Rightarrow Ax \bot \left( {SIE} \right) \Rightarrow Ax \bot IK\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow IK \bot \left( {SAx} \right)\). Khi đó \(d\left( {I;\left( {SAx} \right)} \right) = IK\)
Gọi $F$ là hình chiếu của \(I\) trên \(BD\), ta dễ dàng chứng minh được \(\Delta IAE = \Delta IDF\left( {ch - gn} \right) \) \(\Rightarrow IE = IF = \dfrac{{AO}}{2} = \dfrac{{a\sqrt 2 }}{4}\)
Tam giác vuông \(SIE\), có \(IK = \dfrac{{SI.IE}}{{\sqrt {S{I^2} + I{E^2}} }} = \dfrac{{a\sqrt {21} }}{{14}}\)
Vậy \(d\left( {BD;SA} \right) = 2IK = \dfrac{{a\sqrt {21} }}{7}.\)
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, gọi $I$ là trung điểm của $AB$. Hình chiếu vuông góc của $S$ trên mặt đáy là trung điểm của $CI.$ Biết chiều cao của khối chóp là $a\sqrt 3 .$ Khoảng cách giữa hai đường thẳng $AB$ và $SC$ là :
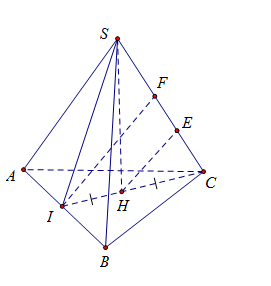
Ta có $\left\{ \begin{array}{l}CI \bot AB\\SH \bot AB\end{array} \right. \Rightarrow AB \bot \left( {SIC} \right)$
Dựng $IF \bot SC\,\,\left( 1 \right)$ khi đó \(IF \subset \left( {SIC} \right) \Rightarrow IF \bot AB\,\,\left( 2 \right)\), do đó $IF$ là đoạn vuông góc chung của $AB$ và $SC$. Dựng $HE \bot SC \Rightarrow HE//IF$ ta có: $HE = \dfrac{1}{2}IF$
Lại có $CI = \dfrac{{a\sqrt 3 }}{2} \Rightarrow CH = \dfrac{{a\sqrt 3 }}{4}$
Khi đó
$HE = \dfrac{{SH.HC}}{{\sqrt {S{H^2} + C{H^2}} }} = \dfrac{{a\sqrt 3 .\dfrac{{a\sqrt 3 }}{4}}}{{\sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {{\left( {\dfrac{{a\sqrt 3 }}{4}} \right)}^2}} }} = \dfrac{{a\sqrt {51} }}{{17}} \Rightarrow IF = \dfrac{{2a\sqrt {51} }}{{17}}$.

