Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật, biết \(AB = 2a,\,\,AD = a,\,\,SA = 3a\) và \(SA\) vuông góc với mặt phẳng đáy. Gọi \(M\) là trung điểm cạnh \(CD\). Khoảng cách giữa hai đường thẳng \(SC\) và \(BM\) bằng:
Trả lời bởi giáo viên
Đáp án đúng: b
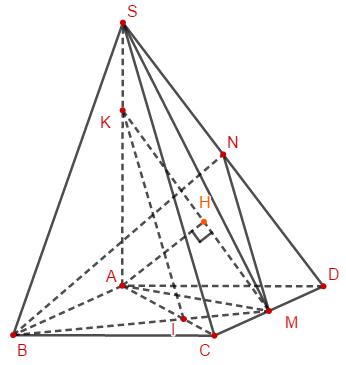
Gọi I là giao điểm của MB và AC, kẻ \(IK//SC\left( {K \in SA} \right)\), kẻ \(MN//SC\left( {N \in S{\rm{D}}} \right)\). Khi đó \(KI,MN \subset \left( {BMN} \right)\). Kẻ \(AH \bot KM\)
Do ABCD là hình chữ nhật có AB=2CD nên \(AM \bot BM \Rightarrow BM \bot \left( {SAM} \right)\)
\( \Rightarrow \left( {BMN} \right) \bot \left( {SAM} \right) \Rightarrow AH \bot \left( {BMN} \right)\)
Ta có AI=2CI (vì CM//AB và AB=2CM)
Suy ra AK=2KS và
\(\begin{array}{l}d\left( {SC,BM} \right) = d\left( {SC,\left( {BMN} \right)} \right) = d\left( {C,\left( {BMN} \right)} \right)\\ = \dfrac{1}{2}d\left( {A,\left( {BMN} \right)} \right) = \dfrac{1}{2}AH\end{array}\)
\(\begin{array}{l}AK = \dfrac{2}{3}SA = 2{\rm{a}};AM = AD\sqrt 2 = a\sqrt 2 \\ \Rightarrow \dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{K^2}}} + \dfrac{1}{{A{M^2}}} = \dfrac{1}{{4{{\rm{a}}^2}}} + \dfrac{1}{{2{{\rm{a}}^2}}} = \dfrac{3}{{4{{\rm{a}}^2}}}\\ \Rightarrow AH = \dfrac{{2a\sqrt 3 }}{3}\end{array}\)
Hướng dẫn giải:
Dựng mặt phẳng \((\alpha )\) chứa \(BM\) và song song \(SC\).
Khi đó $d\left( {BM,SC} \right) = d\left( {SC,\left( \alpha \right)} \right)$
