Cho hình lăng trụ đứng \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\) có đáy $A B C$ là tam giác cân tại \(C,AB = \) \(A{A^\prime } = a\). Góc giữa đường thẳng \(B{C^\prime }\) và mặt phẳng \(\left( {AB{B^\prime }{A^\prime }} \right)\) bằng \({60^0}\). Gọi $M, N, P$ lần lượt là trung điểm của đoạn \(B{B^\prime },C{C^\prime }\) và $B C$. Tính khoảng cách giữa $A M$ và $N P$.

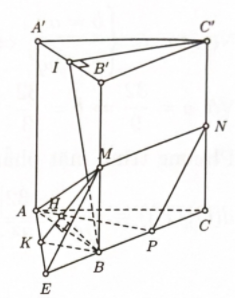
Bước 1: Gọi \(I\) là trung điểm \({A^\prime }{B^\prime }\). Tính BI, BC

Gọi \(I\) là trung điểm \({A^\prime }{B^\prime }\)\( \Rightarrow {C^\prime }I \bot {A^\prime }{B^\prime } \Rightarrow {C^\prime }I \bot \left( {AB{B^\prime }{A^\prime }} \right)\).

\(BI = \sqrt {B{B^{\prime 2}} + {B^\prime }{I^2}}  = \dfrac{{a\sqrt 5 }}{2} \cdot B{C^\prime }\)\( = \dfrac{{BI}}{{\cos \widehat {{C^\prime }BI}}} = a\sqrt 5 \)

\(BC = \sqrt {B{C^{\prime 2}} - C{C^{\prime 2}}}  = 2a\).

Bước 2: Gọi \(E\) là điểm sao cho \(B\) là trung điểm $E P$. Chứng minh \(d(AM,NP)\)\( = 2d(B;(AME))\).

Gọi \(E\) là điểm sao cho \(B\) là trung điểm $E P$.

\( \Rightarrow MNPE\) là hình bình hành \( \Rightarrow EM//NP\)

\( \Rightarrow d(AM,NP) = d(P;(AME))\)\( = 2d(B;(AME))\).

Bước 3: Tính \(d(AM,NP)\)

Ké \(BK \bot AE(K \in AE),BH \bot MK(H \in KM)\)

\( \Rightarrow AE \bot \left( {BMK} \right) \Rightarrow AE \bot BH\)\( \Rightarrow BH \bot \left( {AME} \right)\)

\( \Rightarrow d(B,(AME)) = BH.\)

Tam giác $A P E$ có \(AB = BP = BE = a\)

\( \Rightarrow \Delta APE\) vuông ở \(A\)

\( \Rightarrow BK//AP\).

Mà \(B\) là trung điểm \(EP\)\( \Rightarrow KB = \dfrac{1}{2}AP\).

Ta có: \(A{P^2} = \dfrac{{A{B^2} + A{C^2}}}{2} - \dfrac{{B{C^2}}}{4}\)\( \Rightarrow AP = \dfrac{{a\sqrt 6 }}{2} \Rightarrow BK = \dfrac{{a\sqrt 6 }}{4}\).

\(BH = \dfrac{{BK.BM}}{{\sqrt {B{K^2} + B{M^2}} }} = \dfrac{{a\sqrt {15} }}{{10}}\)\( \Rightarrow d(AM,NP) = \dfrac{{a\sqrt {15} }}{5}\)