Cho tứ diện ABCD có \(\widehat {ABC} = \widehat {ADC} = \widehat {BCD} = {90^0 },BC = 2a,CD = a\), góc giữa đường thẳng AB và mặt phẳng \((BCD)\) bằng \({60^0}\). Tính khoảng cách giữa hai đường thẳng AC và BD.

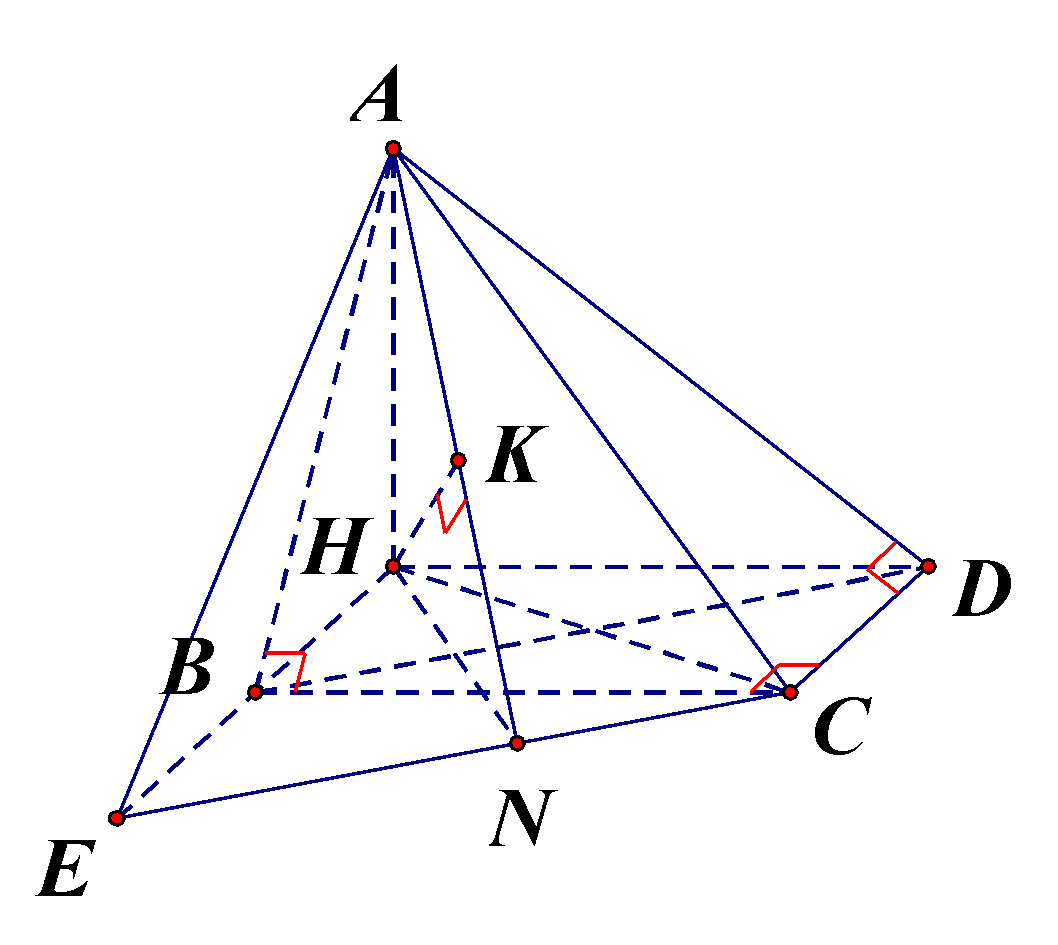
Bước 1: Gọi \(H\) là hình chiếu vuông góc của \(A\) lên mặt phẳng \((BCD)\). Chứng minh HBCD là hình chữ nhật và tìm các cạnh của tứ giác.

Gọi \(H\) là hình chiếu vuông góc của \(A\) lên mặt phẳng \((BCD)\).

\({\rm{ Do }}\left\{ {\begin{array}{*{20}{l}}{BC \bot AB}\\{BC \bot AH,({\rm{ do }}AH \bot (BCD))}\end{array}} \right.\)

\( \Rightarrow BC \bot (ABH) \Rightarrow BC \bot BH(1)\)

Tương tự \(\left\{ {\begin{array}{*{20}{l}}{CD \bot AD}\\{CD \bot AH,({\rm{ do }}AH \bot (BCD))}\end{array}} \right.\)

\( \Rightarrow CD \bot (ADH) \Rightarrow CD \bot DH(2)\)

Ta có \(\widehat {BCD} = {90^0 }\). (3)

Từ (1), (2), (3) nên tứ giác HBCD là hình chữ nhật có \(BC = HD = 2a;HB = DC = a\) và \((\widehat {AB,(BCD)}) = \overline {(AB,BH)}  = \widehat {ABH} = {60^0}\).

Bước 2: Gọi \(E\) là đỉnh của hình bình hành BDCE. HN là đường cao tam giác HEC. Chứng minh \(d(AC,BD) = \dfrac{1}{2}HK\)

Gọi \(E\) là đỉnh của hình bình hành BDCE.

Khoảng cách giữa hai đường thẳng AC và BD bằng

\(d(AC,BD) = d(BD,(AEC))\)\( = d(B,(AEC)) = \dfrac{1}{2}d(H,(AEC))\).

Gọi HN là đường cao tam giác HEC, đường thẳng HK là đường cao tam giác AHN.

Ta có \(\left\{ {\begin{array}{*{20}{l}}{CE \bot HN}\\{CE \bot AH,({\rm{ do }}AH \bot (BCD))}\end{array}} \right.\)

\( \Rightarrow CE \bot (AHN) \Rightarrow CE \bot HK\) và \(AN \bot HK\) nên \(HK \bot (AEC)\).

Vậy \(d(AC,BD) = \dfrac{1}{2}d(H,(AEC)) = \dfrac{1}{2}HK\).

Bước 3: Tính \(d(AC,BD)\)

Trong \(\Delta HEC\) có \(HE.BC = EC.HN\)\( \Rightarrow HN = \dfrac{{HE.BC}}{{EC}} = \dfrac{{4a}}{{\sqrt 5 }}\).

Trong \(\Delta AHN\) có \(\dfrac{1}{{H{K^2}}} = \dfrac{1}{{H{A^2}}} + \dfrac{1}{{H{N^2}}}\)\( = \dfrac{1}{{3{a^2}}} + \dfrac{5}{{16{a^2}}} = \dfrac{{31}}{{48{a^2}}}\)\( \Rightarrow HK = \dfrac{{4\sqrt 3 a}}{{\sqrt {31} }}\)

Vậy \(d(AC,BD) = \dfrac{1}{2}HK = \dfrac{{2\sqrt 3 a}}{{\sqrt {31} }}\).