Câu hỏi:
2 năm trước
Cho hình chóp $S . A B C$ có đáy $A B C$ là tam giác vuông cân tại \(A,AB = a\), $S A$ vuông góc với mặt phẳng đáy và \(SA = \sqrt 3 a\). Gọi \(M\) là trung điểm $B C$. Khoảng cách giữa hai đường thẳng $A C$ và $S M$ bằng
Trả lời bởi giáo viên
Đáp án đúng: c
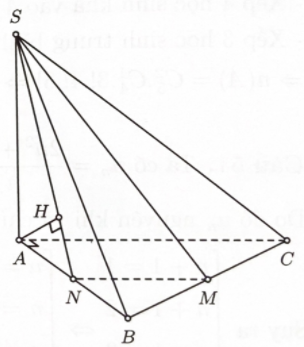
Gọi \(N\) là trung điểm $A B$. Kẻ \(AH \bot SN\).
Vì \(MN//AC,MN \subset (SMN)\) nên \(AC//(SMN)\)
\( \Rightarrow d(SM;AC) = d(AC;(SMN))\)\( = d(A;(SMN))\)
Ta có \(\left\{ {\begin{array}{*{20}{l}}{MN \bot AB}\\{MN \bot SA}\end{array}} \right.\)\( \Rightarrow MN \bot (SAB) \Rightarrow MN \bot AH\).
Từ đó suy ra \(AH \bot (SMN)\)\( \Rightarrow d(SM;AC) = AH\).
Lại có \(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{S^2}}} + \dfrac{1}{{A{N^2}}} = \dfrac{{13}}{{3{a^2}}}\)\( \Rightarrow AH = \dfrac{{\sqrt {39} a}}{{13}}\).
Hướng dẫn giải:
Bước 1: Gọi \(N\) là trung điểm $A B$. Kẻ \(AH \bot SN\).
Bước 2: Chứng minh \(d(SM;AC) = d(A;(SMN))\)
Bước 3: Tính AH.
