Cho hình hộp chữ nhật \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có \(AB = a,AD = 2a,A{A^\prime } = a\). Gọi \(M\) là điểm trên đoạn $A D$ với \(\dfrac{{AM}}{{MD}} = 3\). Gọi \(x\) là độ dài khoảng cách giữa hai đường thẳng \(A{D^\prime },{B^\prime }C\) và \(y\) là độ dài khoảng cách từ \(M\) đến mặt phẳng \(\left( {A{B^\prime }C} \right)\). Tính giá trị $x y$.

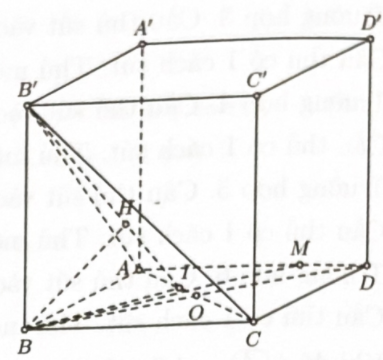
Bước 1: \(d\left( {M,\left( {A{B^\prime }C} \right)} \right) = \dfrac{3}{4}d\left( {B;\left( {A{B^\prime }C} \right)} \right)\)

Ta có \({B^\prime }C//{A^\prime }D \Rightarrow {B^\prime }C//\left( {AD{D^\prime }{A^\prime }} \right) \supset A{D^\prime }\)

\( \Rightarrow d\left( {{B^\prime }C,A{D^\prime }} \right) = d\left( {C,\left( {AD{D^\prime }{A^\prime }} \right)} \right) = CD = a.\)

Suy ra \(x = a\). Lại có \(\dfrac{{MA}}{{DA}} = \dfrac{3}{4}\) .

\( \Rightarrow d\left( {M,\left( {A{B^\prime }C} \right)} \right) = \dfrac{3}{4}d\left( {D,\left( {A{B^\prime }C} \right)} \right) = \dfrac{3}{4}d\left( {B;\left( {A{B^\prime }C} \right)} \right)\).

Bước 2: Gọi I là hình chiếu vuông góc của \(B\) lên $A C$

Gọi I là hình chiếu vuông góc của \(B\) lên $A C$ ta có: \(\left\{ {\begin{array}{*{20}{l}}{AC \bot BI}\\{AC \bot B{B^\prime }}\end{array} \Rightarrow AC \bot \left( {B{B^\prime }I} \right)} \right.\)

Bước 3: Gọi \(H\) là hình chiếu của \(B\) lên \({B^\prime }I\)

Gọi \(H\) là hình chiếu của \(B\) lên \({B^\prime }I\) ta có: \(\left\{ {\begin{array}{*{20}{l}}{BH \bot {B^\prime }I}\\{BH \bot AC}\end{array} \Rightarrow BH \bot \left( {{B^\prime }AC} \right) \Rightarrow d\left( {B,\left( {A{B^\prime }C} \right)} \right) = BH.} \right.\) Trong tam giác $A B C$, ta có: \(AB \cdot BC = AC \cdot BI \Rightarrow BI = \dfrac{{AB \cdot BC}}{{AC}} = \dfrac{{a \cdot 2a}}{{a\sqrt 5 }} = \dfrac{{2a\sqrt 5 }}{5}\). Trong tam giác \(B{B^\prime }I\), ta có: \(\dfrac{1}{{B{H^2}}} = \dfrac{1}{{B{I^2}}} + \dfrac{1}{{B{B^{\prime 2}}}} \Rightarrow BH = \dfrac{{BI \cdot B{B^\prime }}}{{\sqrt {B{I^2} + B{B^{\prime 2}}} }} = \dfrac{{2a}}{3}\) \( \Rightarrow d\left( {M,\left( {A{B^\prime }C} \right)} \right) = \dfrac{3}{4} \cdot \dfrac{{2a}}{3} = \dfrac{a}{2}.\) Suy ra \(y = \dfrac{a}{2}.\) Vậy \(xy = \dfrac{{{a^2}}}{2}\).