Câu hỏi:
2 năm trước
Cho tứ diện đều $A B C D$ có cạnh bằng \(\sqrt {11} \). Gọi \(I\) là trung điểm cạnh $C D$. Tính khoảng cách giữa hai đường thẳng $A C$ và $B I$.
Trả lời bởi giáo viên
Đáp án đúng: d
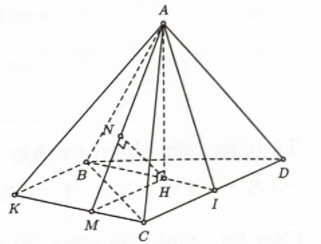
Bước 1: Dựng hình bình hành \(BICK\). Gọi \(H\) là tâm \(\Delta BCD\). Vẽ \(HM \bot KC\) tại \(M,HN \bot AM\) tại \(N\).
Dựng hình bình hành \(BICK\)
\( \Rightarrow BICK\) là hình chữ nhật do \(BI \bot CD\).
Gọi \(H\) là tâm \(\Delta BCD\).
Vẽ \(HM \bot KC\) tại \(M,HN \bot AM\) tại \(N\).
Bước 2: Chứng minh \(d(AC,BI) = HN\)
Ta có \(CK \bot (AHM) \Rightarrow CK \bot HN\)\( \Rightarrow HN \bot (ACK)\).
Ta có \(BI//(ACK)\)
\( \Rightarrow d(AC,BI) = d(BI,(ACK))\)\( = d(H,(ACK)) = HN.\)
Bước 3: Tính HN
Xét tam giác vuông \(ABH\) có \(AH = \sqrt {A{B^2} - B{H^2}} \)\( = \sqrt {11 - {{\left( {\dfrac{{\sqrt {11} \cdot \sqrt 3 }}{3}} \right)}^2}} = \dfrac{{\sqrt {66} }}{3}\)
Ta có \(HM = CI = \dfrac{{\sqrt {11} }}{2}\) (vì $B I C K$ là hình chữ nhật)
Xét \(\Delta AHM\) vuông có \(HN = \dfrac{{AH.HM}}{{\sqrt {A{H^2} + H{M^2}} }} = \dfrac{{\dfrac{{\sqrt {66} }}{3} \cdot \dfrac{{\sqrt {11} }}{2}}}{{\sqrt {\dfrac{{22}}{3} + \dfrac{{11}}{4}} }}\)\( = \sqrt 2 \)\( \Rightarrow d(AC,BI) = \sqrt 2 \).
Hướng dẫn giải:
Bước 1: Dựng hình bình hành \(BICK\). Gọi \(H\) là tâm \(\Delta BCD\). Vẽ \(HM \bot KC\) tại \(M,HN \bot AM\) tại \(N\).
Bước 2: Chứng minh \(d(AC,BI) = HN\)
Bước 3: Tính HN
