Câu hỏi:
2 năm trước
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a tâm O, \(SA \bot \left( {ABCD} \right)\) và \(SA = a\sqrt 6 \). Tính khoảng cách giữa hai đường thẳng SO và BC.
Trả lời bởi giáo viên
Đáp án đúng: b
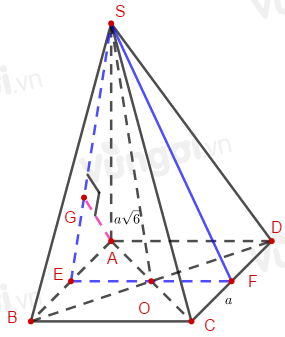
Bước 1:
Gọi E, F lần lượt là trung điểm của AB và CD.
=> EF//BC
=> BC//(SEF)
Bước 2:
Mà \(O \in EF\)\( \Rightarrow SO \subset \left( {SEF} \right)\)
\(\begin{array}{l} \Rightarrow d\left( {BC,SO} \right) = d\left( {BC,\left( {SEF} \right)} \right)\\ = d\left( {B,\left( {SEF} \right)} \right) = d\left( {A,\left( {SEF} \right)} \right)\end{array}\)
Bước 3:
Kẻ AG vuông góc với SE.
Ta có \(EF\parallel AD,AD \bot AB \Rightarrow EF \bot AB\)
Mà \(EF \bot SA\)
\(\begin{array}{l}\left. \begin{array}{l} \Rightarrow EF \bot \left( {SAB} \right) \Rightarrow \left( {SEF} \right) \bot \left( {SAB} \right)\\\left( {SEF} \right) \cap \left( {SAB} \right) = SE\\AG \subset \left( {SAB} \right),AG \bot SE\end{array} \right\}\\ \Rightarrow AG \bot \left( {SEF} \right)\\ = > d\left( {A,\left( {SEF} \right)} \right) = AG\end{array}\)
Bước 4:
Ta có \(AE = \dfrac{{AB}}{2} = \dfrac{a}{2};SA = a\sqrt 6 \).
\(\begin{array}{l}\dfrac{1}{{A{G^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{E^2}}} = \dfrac{1}{{6{a^2}}} + \dfrac{4}{{{a^2}}} = \dfrac{{25}}{{6{a^2}}}\\ = > d\left( {BC,SO} \right) = AG = \dfrac{{a\sqrt 6 }}{5}\end{array}\)
Hướng dẫn giải:
Bước 1: Gọi E, F lần lượt là trung điểm của AB và CD. Chứng minh BC//(SEF).
Bước 2: Sử dụng các mối quan hệ về song song để tìm mối liên hệ giữa \(d\left( {SO,BC} \right)\) và \(d\left( {A,\left( {SEF} \right)} \right)\)
Bước 3: Kẻ AG vuông góc với SE, chứng minh \(d\left( {A,\left( {SEF} \right)} \right) = AG\).
Bước 4: Tính AG.
