Cho tam giác \(ABC\) cân tại \(A\) có \(AB = 10cm,\,\,BC = 12cm\), đường cao \(AH\). Gọi \(E,F\) lần lượt là hình chiếu của \(H\) trên \(AB\) và \(AC\). Gọi \(I\) là giao điểm của \(AH\) và \(EF\).
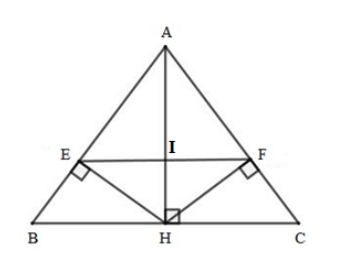
Tính \(HE\).
Ta có: \(H\) là trung điểm của \(BC\) (vì \(AH\) là đường trung tuyến) nên \(BH = \dfrac{1}{2}BC = 6\,cm\).
Áp dụng định lí Pitago trong tam giác vuông \(AHB\) ta có:
\(\begin{array}{l}A{H^2} + B{H^2} = A{B^2}\\ \Rightarrow A{H^2} = A{B^2} - B{H^2} = {10^2} - {6^2} = 64\\ \Rightarrow AH = 8\,cm\end{array}\)
Lại có: (chứng minh câu a)
\( \Rightarrow \dfrac{{EH}}{{HB}} = \dfrac{{AH}}{{AB}} \Rightarrow EH = \dfrac{{HB.AH}}{{AB}} = \dfrac{{6.8}}{{10}} = 4,8\,cm\).
Vậy \(HE = 4,8\,cm.\)
Cho tam giác \(ABC\) cân tại \(A\) có \(AB = 10cm,\,\,BC = 12cm\), đường cao \(AH\). Gọi \(E,F\) lần lượt là hình chiếu của \(H\) trên \(AB\) và \(AC\). Gọi \(I\) là giao điểm của \(AH\) và \(EF\).

Tính diện tích tam giác \(AEF\) (làm tròn đến hàng đơn vị).
Theo câu trước ta có: \(EF//BC\) nên \(\widehat {AEF} = \widehat {ABC}\) (hai góc đồng vị) và \(EH = 4,8\,cm\).
Xét \(\Delta AEF\) và \(\Delta ABC\) ta có:
\(\widehat {EAF}\,chung\)
\(\widehat {AEF} = \widehat {ABC}\) (cmt)
\( \Rightarrow \Delta AEF \backsim \Delta ABC\,\,\left( {g - g} \right).\)
\( \Rightarrow \dfrac{{AE}}{{AB}} = \dfrac{{AF}}{{AC}} = \dfrac{{EF}}{{BC}}\) (các cặp cạnh tương ứng)
Áp dụng định lý Pi-ta-go cho \(\Delta AEH\) ta có: \(AE = \sqrt {A{H^2} - E{H^2}} = \sqrt {{8^2} - 4,{8^2}} = 6,4\,\,cm.\)
\(\begin{array}{l} \Rightarrow \dfrac{{AE}}{{AB}} = \dfrac{{6,4}}{{10}} = \dfrac{{16}}{{25}}.\\ \Rightarrow \dfrac{{{S_{\Delta AEF}}}}{{{S_{\Delta ABC}}}} = {\left( {\dfrac{{AE}}{{AB}}} \right)^2} = {\left( {\dfrac{{16}}{{25}}} \right)^2}\\ \Rightarrow {S_{\Delta AEF}} = {\left( {\dfrac{{16}}{{25}}} \right)^2}.{S_{\Delta ABC}}\\ = {\left( {\dfrac{{16}}{{25}}} \right)^2}.\dfrac{1}{2}.AH.BC\\ = {\left( {\dfrac{{16}}{{25}}} \right)^2}.\dfrac{1}{2}.8.12\\ = 19,6608\,\,c{m^2}.\end{array}\).
Vậy \({S_{\Delta AEF}} \approx 20\,c{m^2}.\)
Khu vườn hình chữ nhật có chiều dài \(75m,\) chiều rộng bằng một phần ba chiều dài. Tính diện tích của khu vườn?
Chiều rộng khu vườn là: \(\dfrac{1}{3} \times 75 = 25m\).
Diện tích khu vườn là: \(25 \times 75 = 1875{m^2}\)
Đáp số: \(1875\,{m^2}.\)
Tìm số tự nhiên \(x,\) biết: \(\left( {1,2 + 3,7} \right) < x < \left( {2,1 + 3,2} \right)\).
Ta có:
\(\left( {1,2 + 3,7} \right) < x < \left( {2,1 + 3,2} \right)\)
Hay \(4,9 < x < 5,3\).
Nên chỉ có \(x = 5\) thỏa mãn.
Cho ba số dương \(a,\,b,\,c\) có tổng bằng \(1\). Giá trị nhỏ nhất của \(P = \dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c}\) là:
Theo giả thiết ta có: \(a + b + c = 1\).
Ta có:
\(\begin{array}{l}\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} = \dfrac{{a + b + c}}{a} + \dfrac{{a + b + c}}{b} + \dfrac{{a + b + c}}{c}\\ = 1 + \dfrac{b}{a} + \dfrac{c}{a} + \dfrac{a}{b} + 1 + \dfrac{c}{b} + \dfrac{a}{c} + \dfrac{b}{c} + 1\\ = 3 + \left( {\dfrac{b}{a} + \dfrac{a}{b}} \right) + \left( {\dfrac{b}{c} + \dfrac{c}{b}} \right) + \left( {\dfrac{c}{a} + \dfrac{a}{c}} \right)\\ \ge 3 + 2.\sqrt {\dfrac{b}{a} \cdot \dfrac{a}{b}} + 2.\sqrt {\dfrac{b}{c} \cdot \dfrac{c}{b}} + 2.\sqrt {\dfrac{c}{a} \cdot \dfrac{a}{c}} \\ \ge 3 + 2.1 + 2.1 + 2.1 = 9\end{array}\)
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}a = b = c\\a + b + c = 1\end{array} \right. \Leftrightarrow a = b = c = \dfrac{1}{3}.\)
Vậy \(P = \dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} \ge 9\) hay giá trị nhỏ nhất của \(P\) là \(9\) khi \(a = b = c = \dfrac{1}{3}.\)
Có bao nhiêu cặp số nguyên \(\left( {x;\;y} \right)\) thỏa mãn phương trình: \({x^3} + 3x = {x^2}y + 2y + 5.\)
Ta có:
\(\begin{array}{l}\;\;\;\;{x^3} + 3x = {x^2}y + 2y + 5\\ \Leftrightarrow {x^3} + 3x - 5 = {x^2}y + 2y\\ \Leftrightarrow {x^3} + 3x - 5 = y\left( {{x^2} + 2} \right)\\ \Leftrightarrow y = \dfrac{{{x^3} + 3x - 5}}{{{x^2} + 2}}\;\;\left( {do\;\;{x^2} + 2 > 0} \right)\\ \Leftrightarrow y = \dfrac{{{x^3} + 2x + x - 5}}{{{x^2} + 2}}\\ \Leftrightarrow y = x + \dfrac{{x - 5}}{{{x^2} + 2}}\;\;\left( * \right)\;.\end{array}\)
Để \(y \in \mathbb{Z} \Rightarrow \left( {x + \dfrac{{x - 5}}{{{x^2} + 2}}} \right) \in \mathbb{Z}\)
Mà \(x \in \mathbb{Z} \Rightarrow y \in \mathbb{Z} \Leftrightarrow \dfrac{{x - 5}}{{{x^2} + 2}} \in \mathbb{Z} \Leftrightarrow \left( {x - 5} \right)\; \vdots \;\left( {{x^2} + 2} \right)\)
\(\begin{array}{l} \Rightarrow \left[ {\left( {x - 5} \right)\left( {x + 5} \right)} \right]\; \vdots \;\left( {{x^2} + 2} \right)\\ \Leftrightarrow \left( {{x^2} - 25} \right)\; \vdots \;\left( {{x^2} + 2} \right)\\ \Leftrightarrow \left( {{x^2} + 2 - 27} \right)\; \vdots \;\left( {{x^2} + 2} \right)\\ \Leftrightarrow 27\; \vdots \;\left( {{x^2} + 2} \right)\end{array}\).
Hay \(\left( {{x^2} + 2} \right) \in Ư\left( {27} \right)\)
Mà \({x^2} + 2 \ge 2\;\;\forall x \in \mathbb{Z} \Rightarrow \left( {{x^2} + 2} \right) \in \left\{ {3;\;9;\;27} \right\}\)
\( \Leftrightarrow \left[ \begin{array}{l}{x^2} + 2 = 3\\{x^2} + 2 = 9\\{x^2} + 2 = 27\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^2} = 1\;\;\left( {tm} \right)\\{x^2} = 7\;\;\left( {ktm} \right)\\{x^2} = 25\;\;\left( {tm} \right)\end{array} \right. \Rightarrow \left[ \begin{array}{l}{x^2} = 1\\{x^2} = 25\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\;\\x = - 1\;\\x = 5\\x = - 5\end{array} \right.\)
+) Với \(x = 1 \Rightarrow \left( * \right) \Leftrightarrow y = 1 + \dfrac{{1 - 5}}{{1 + 2}} = - \dfrac{1}{3}\;\;\left( {ktm} \right)\)
+) Với \(x = - 1 \Rightarrow \left( * \right) \Leftrightarrow y = - 1 + \dfrac{{ - 1 - 5}}{{{{\left( { - 1} \right)}^2} + 2}} = - 3\;\;\left( {tm} \right)\)
+) Với \(x = 5 \Rightarrow y = x + \dfrac{{x - 5}}{{{x^2} + 2}} = 5 + \dfrac{0}{{27}} = 5\;\;\left( {tm} \right)\)
+) Với \(x = - 5 \Rightarrow y = x + \dfrac{{x - 5}}{{{x^2} + 2}} = - 5 + \dfrac{{ - 5 - 5}}{{27}} = - \dfrac{{145}}{{27}}\;\;\left( {ktm} \right)\)
Vậy có hai cặp số nguyên \(\left( {x;\;y} \right) \in \left\{ {\left( { - 1; - 3} \right);\;\left( {5;\;5} \right)} \right\}\) thỏa mãn phương trình.
Cho hai biểu thức:
\(A = \dfrac{x}{{x - 3}},\)\(B = \dfrac{{2x}}{{x + 5}} - \dfrac{{{x^2} - 15x}}{{{x^2} - 25}}\,\,\,\,\left( {x \ne 0;x \ne 3;x \ne \pm 5} \right)\)
Tính giá trị của biểu thức \(A\) tại \(x\) thỏa mãn \(\left| {x - 2} \right| = 1\).
Điều kiện: \(x \ne 3.\)
Ta có: \(\left| {x - 2} \right| = 1 \Leftrightarrow \left[ \begin{array}{l}x - 2 = 1\\x - 2 = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1 + 2\\x = - 1 + 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\,\,(ktm)\\x = 1\,\,\,(tm)\end{array} \right.\)
Thay \(x = 1\) vào biểu thức \(A\) ta có: \(\dfrac{1}{{1 - 3}} = \dfrac{1}{{ - 2}} = - \dfrac{1}{2}\)
Vậy giá trị của biểu thức \(A\) tại \(x\) thỏa mãn \(\left| {x - 2} \right| = 1\) là \(\dfrac{{ - 1}}{2}\).
Cho hai biểu thức:
\(A = \dfrac{x}{{x - 3}},\)\(B = \dfrac{{2x}}{{x + 5}} - \dfrac{{{x^2} - 15x}}{{{x^2} - 25}}\,\,\,\,\left( {x \ne 0;x \ne 3;x \ne \pm 5} \right)\)
Rút gọn biểu thức \(Q = B:A\) ta được:
Điều kiện: \(x \ne 0,\,\,x \ne 3;\,\,x \ne \pm 5.\)
\(B:A = \left( {\dfrac{{2x}}{{x + 5}} - \dfrac{{{x^2} - 15x}}{{{x^2} - 25}}} \right):\dfrac{x}{{x - 3}}\)\(= \left[ {\dfrac{{2x\left( {x - 5} \right)}}{{\left( {x + 5} \right)\left( {x - 5} \right)}} - \dfrac{{{x^2} - 15x}}{{\left( {x + 5} \right)\left( {x - 5} \right)}}} \right].\dfrac{{x - 3}}{x} \)\(= \dfrac{{2x\left( {x - 5} \right) - \left( {{x^2} - 15x} \right)}}{{\left( {x + 5} \right)\left( {x - 5} \right)}}.\dfrac{{x - 3}}{x}\)\( = \dfrac{{2{x^2} - 10x - {x^2} + 15x}}{{\left( {x + 5} \right)\left( {x - 5} \right)}}.\dfrac{{x - 3}}{x}\)\( = \dfrac{{{x^2} + 5x}}{{\left( {x + 5} \right)\left( {x - 5} \right)}}.\dfrac{{x - 3}}{x}\)\( = \dfrac{{x\left( {x + 5} \right)}}{{\left( {x + 5} \right)\left( {x - 5} \right)}}.\dfrac{{x - 3}}{x}\)\( = \dfrac{x}{{x - 5}}.\dfrac{{x - 3}}{x} = \dfrac{{x - 3}}{{x - 5}}\).
Vậy \(Q = B:A = \dfrac{{x - 3}}{{x - 5}}\).
Cho hai biểu thức:
\(A = \dfrac{x}{{x - 3}},\)\(B = \dfrac{{2x}}{{x + 5}} - \dfrac{{{x^2} - 15x}}{{{x^2} - 25}}\,\,\,\,\left( {x \ne 0;x \ne 3;x \ne \pm 5} \right)\)
Cho \(Q = B:A.\) Tìm \(x\) để \(Q = 3.\)
Theo câu trước ta có: \(Q = B:A = \dfrac{{x - 3}}{{x - 5}}\) với \(x \ne 0,\,\,x \ne 3;\,\,x \ne \pm 5.\)
Để \(Q = 3\) thì \(\dfrac{{x - 3}}{{x - 5}} = 3 \Rightarrow x - 3 = 3\left( {x - 5} \right)\)
\( \Leftrightarrow x - 3 = 3x - 15 \Leftrightarrow 2x = 12 \Leftrightarrow x = 6\left( {tm} \right)\).
Cho hai biểu thức:
\(A = \dfrac{x}{{x - 3}},\)\(B = \dfrac{{2x}}{{x + 5}} - \dfrac{{{x^2} - 15x}}{{{x^2} - 25}}\,\,\,\,\left( {x \ne 0;x \ne 3;x \ne \pm 5} \right)\)
Tìm \(x\) để \(Q =B:A> 1\).
Ta có: \(Q = \dfrac{{x - 3}}{{x - 5}} = \dfrac{{x - 5 + 2}}{{x - 5}} \)\(= 1 + \dfrac{2}{{x - 5}}\)
Do đó để \(Q > 1\) thì \(1 + \dfrac{2}{{x - 5}} > 1 \Leftrightarrow \dfrac{2}{{x - 5}} > 0\)\( \Leftrightarrow x - 5 > 0 \Leftrightarrow x > 5\,\,\,(tmdk)\)
Vậy với \(x > 5\) thì \(Q > 1\).
Một khối kim loại hình lập phương có cạnh 1m, mỗi đề-xi-mét khối kim loại đó cân nặng 5kg. Hỏi khối kim loại đó cân nặng bao nhiêu tấn?
Thể tích khối kim loại là: \(1 \times 1 \times 1 = 1{m^3} = 1000d{m^3}\).
Khối lượng khối kim loại là: \(1000 \times 5 = 5000kg = 5\) tấn.
Đáp số: \(5\)tấn.
Một thửa ruộng hình bình hành có số đo cạnh đáy là \(120\,m\) và chiều cao bằng \(\dfrac{3}{4}\) cạnh đáy. Người ta cấy lúa trên thửa ruộng đó, cứ \(50\,{m^2}\) thu được \(1250\,kg\) lúa. Hỏi thửa ruộng đó thu được bao nhiêu tấn lúa?
Chiều cao của hình bình hành là: \(\dfrac{3}{4} \times 120 = 90\,m\).
Diện tích hình bình hành là: \(90 \times 120 = 10800\,{m^2}\).
\(1{m^2}\) thu hoạch được số kg lúa là: \(1250:500 = 2,5\,kg\).
Thửa ruộng thu hoạch được số kg lúa là: \(10800 \times 2,5 = 27000\,kg\).
Đổi: \(270000kg = 27\) tấn. Nên thửa ruộng thu hoạch được \(27\) tấn lúa.
Đáp số: \(27\) tấn.
Hình tam giác có độ dài đáy \(\dfrac{5}{7}\) cm và chiều cao bằng \(\dfrac{3}{5}\) độ dài đáy. Tính diện tích tam giác đó?
Chiều cao tam giác là: \(\dfrac{3}{5} \times \dfrac{5}{7} = \dfrac{3}{7}\,cm\).
Diện tích tam giác là: \(\dfrac{1}{2} \times \dfrac{5}{7} \times \dfrac{3}{7} = \dfrac{{15}}{{98}}\,c{m^2}\).
Đáp số: \(\dfrac{{15}}{{98}}\,c{m^2}.\)
Hình vuông \(ABCD\) có diện tích bằng \(16c{m^2}.\) Hai điểm \(E,F\) lần lượt là trung điểm của cạnh \(AB,AD.\) Khi đó diện tích hình thang \(EBDF\) là:
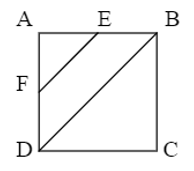
Diện tích hình vuông bằng \(16\,c{m^2}\) nên cạnh hình vuông bằng \(4\,cm\) (vì \(4 \times 4 = 16\)).
Suy ra: \(AB = AD = BC = DC = 4cm\).
Độ dài \(AE\) là: \(AB:2 = 4:2 = 2cm\).
Độ dài \(AF\) là: \(AD:2 = 4:2 = 2\,cm\).
Diện tích tam giác \(AEF\) là: \(\dfrac{1}{2} \times AE \times AF = \dfrac{1}{2} \times 2 \times 2 = 2c{m^2}\).
Diện tích tam giác \(BDC\) là: \(\dfrac{1}{2} \times CD \times CB = \dfrac{1}{2} \times 4 \times 4 = 8c{m^2}\).
Diện tích hình thang \(EBDF\) là: \({S_{ABCD}} - {S_{AEF}} - {S_{BDC}}\)\( = 16 - 2 - 8 = 6\,c{m^2}.\)
Đáp số: \(6\,c{m^2}.\)
Cho tam giác \(ABC\) có diện tích \(160\,c{m^2}.\) Gọi \(M,N\) theo thứ tự là đểm thuộc các cạnh \(AB,AC\) sao cho \(AM = \dfrac{1}{4}AB,\,AN = \dfrac{1}{4}AC.\) Tính diện tích tam giác \(AMN.\)
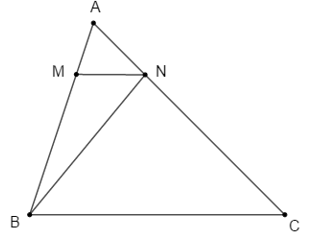
Nhận thấy hai tam giác \(ABN\) và \(ABC\) có chung chiều cao hạ từ đỉnh \(B\).
Mà \(AN = \dfrac{1}{4} \times AC\) nên \({S_{{\rm{ABN}}}} = \dfrac{1}{4}{S_{ABC}}{\rm{ }}\).
Nhận thấy hai tam giác \(AMN\) và \(ABN\) có chung chiều cao hạ từ đỉnh \(N\) mà \(AM = \dfrac{1}{4} \times AB\) nên \({{\rm{S}}_{{\rm{AMN}}}} = \dfrac{1}{4} \times {\rm{ }}{{\rm{S}}_{{\rm{ABN}}}}\).
Do đó: \({S_{AMN}} = \dfrac{1}{4} \times {S_{ABN}}\)\( = \dfrac{1}{4} \times \dfrac{1}{4} \times {S_{ABC}} = \dfrac{1}{{16}} \times {\rm{ }}{{\rm{S}}_{{\rm{ABC}}}}\)\( = \dfrac{1}{{16}}.160 = 10\,c{m^2}.\)
Đáp số: \({S_{AMN}} = 10\,c{m^2}\).
Hình chữ nhật \(ABCD\) có diện tích \(3600c{m^2}\). \(E\) là trung điểm của \(DC.\) Tính diện tích tam giác \(ADE.\)
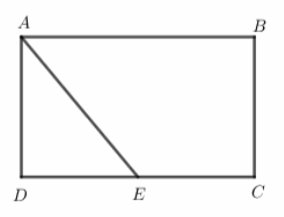
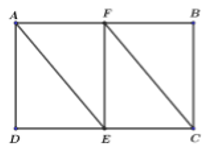
Lấy F là trung điểm của AB, nối \(EF\), \(FC\).
Hình chữ nhật ABCD được phân thành 4 hình tam giác có diện tích bằng nhau và bằng diện tích tam giác \(ADE\).
Vậy diện tích tam giác \(ADE\) là: \(3600:4 = 900\,\left( {c{m^2}} \right)\).
Đáp số: \(900\,c{m^2}\).
Biết \(4\) số tự nhiên liên tiếp có tích bằng \(24024.\) Số lớn nhất trong bốn số đó là:
Ta thấy trong \(4\) số tự nhiên liên tiếp cần tìm thì không có thừa số nào có chữ số tận cùng là \(0;{\rm{ }}5\) vì như thế tích sẽ tận cùng là chữ số \(0\) (trái với bài toán)
Do đó \(4\) số phải tìm chỉ có thể có chữ số tận cùng liên tiếp là \(1,{\rm{ }}2,{\rm{ }}3,{\rm{ }}4\) hoặc \(6,{\rm{ }}7,{\rm{ }}8,{\rm{ }}9\).
Ta có:
\(24024 > 10000 = 10 \times 10 \times 10 \times 10\)
\(24024 < 160000 = 20 \times 20 \times 20 \times 20\)
Nên bốn số phải tìm phải là số có hai chữ số và có chữ số hàng chục là \(1.\)
Nếu 4 số phải tìm là \(11;{\rm{ 1}}2;{\rm{ 1}}3;{\rm{ 1}}4\) thì: \(11 \times 12 \times 13 \times 14 = 24024\) (đúng)
Nếu 4 số phải tìm là \(6;{\rm{ }}7;{\rm{ }}8;{\rm{ }}9\) thì: \(16 \times 17 \times 18 \times 19 = 93024 > 24024\) (loại)
Vậy 4 số phải tìm là \(11;{\rm{ 12}};{\rm{ 13}};{\rm{ 14}}.\)

