Câu hỏi:
2 năm trước
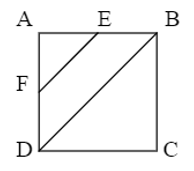
Hình vuông \(ABCD\) có diện tích bằng \(16c{m^2}.\) Hai điểm \(E,F\) lần lượt là trung điểm của cạnh \(AB,AD.\) Khi đó diện tích hình thang \(EBDF\) là:
Trả lời bởi giáo viên
Đáp án đúng: a
Diện tích hình vuông bằng \(16\,c{m^2}\) nên cạnh hình vuông bằng \(4\,cm\) (vì \(4 \times 4 = 16\)).
Suy ra: \(AB = AD = BC = DC = 4cm\).
Độ dài \(AE\) là: \(AB:2 = 4:2 = 2cm\).
Độ dài \(AF\) là: \(AD:2 = 4:2 = 2\,cm\).
Diện tích tam giác \(AEF\) là: \(\dfrac{1}{2} \times AE \times AF = \dfrac{1}{2} \times 2 \times 2 = 2c{m^2}\).
Diện tích tam giác \(BDC\) là: \(\dfrac{1}{2} \times CD \times CB = \dfrac{1}{2} \times 4 \times 4 = 8c{m^2}\).
Diện tích hình thang \(EBDF\) là: \({S_{ABCD}} - {S_{AEF}} - {S_{BDC}}\)\( = 16 - 2 - 8 = 6\,c{m^2}.\)
Đáp số: \(6\,c{m^2}.\)
Hướng dẫn giải:
Tính cạnh hình vuông.
Tính diện tích tam giác \(AEF\) bằng \(\dfrac{1}{2} \times AE \times AF\).
Tính diện tích tam giác \(BDC\) bằng \(\dfrac{1}{2} \times CD \times CB\).
Tính diện tích \(EFDB\) bằng \({S_{ABCD}} - {S_{AEF}} - {S_{BDC}}\).
Câu hỏi khác
- Đề thi khảo sát chất lượng đầu năm - Đề số 1 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 2 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 4 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 5 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 3 toán 9 có lời giải
