Câu hỏi:
2 năm trước
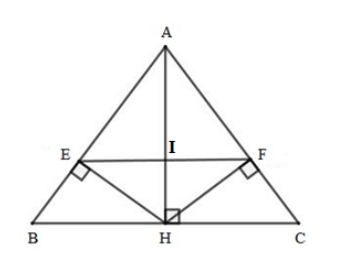
Cho tam giác \(ABC\) cân tại \(A\) có \(AB = 10cm,\,\,BC = 12cm\), đường cao \(AH\). Gọi \(E,F\) lần lượt là hình chiếu của \(H\) trên \(AB\) và \(AC\). Gọi \(I\) là giao điểm của \(AH\) và \(EF\).
Tính \(HE\).
Trả lời bởi giáo viên
Đáp án đúng: d
Ta có: \(H\) là trung điểm của \(BC\) (vì \(AH\) là đường trung tuyến) nên \(BH = \dfrac{1}{2}BC = 6\,cm\).
Áp dụng định lí Pitago trong tam giác vuông \(AHB\) ta có:
\(\begin{array}{l}A{H^2} + B{H^2} = A{B^2}\\ \Rightarrow A{H^2} = A{B^2} - B{H^2} = {10^2} - {6^2} = 64\\ \Rightarrow AH = 8\,cm\end{array}\)
Lại có: (chứng minh câu a)
\( \Rightarrow \dfrac{{EH}}{{HB}} = \dfrac{{AH}}{{AB}} \Rightarrow EH = \dfrac{{HB.AH}}{{AB}} = \dfrac{{6.8}}{{10}} = 4,8\,cm\).
Vậy \(HE = 4,8\,cm.\)
Hướng dẫn giải:
Từ các tam giác đồng dạng, ta suy ra các tỉ lệ tương ứng, từ đó tính được độ dài cạnh HE.
Câu hỏi khác
- Đề thi khảo sát chất lượng đầu năm - Đề số 1 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 2 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 4 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 5 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 3 toán 9 có lời giải
