Giá trị của phân thức \(\dfrac{{{x^2} - 1}}{{{x^2} + 2x + 1}}\) bằng \(0\) khi \(x\) bằng:
Từ yêu cầu đề bài suy ra: \(\dfrac{{{x^2} - 1}}{{{x^2} + 2x + 1}} = 0\)
ĐKXĐ: \(x \ne - 1\)
\(\begin{array}{l}\dfrac{{{x^2} - 1}}{{{x^2} + 2x + 1}} = 0 \Leftrightarrow \dfrac{{\left( {x - 1} \right)\left( {x + 1} \right)}}{{{{\left( {x + 1} \right)}^2}}} = 0\\ \Leftrightarrow \dfrac{{x - 1}}{{x + 1}} = 0 \Leftrightarrow x - 1 = 0 \Leftrightarrow x = 1\,\,(tmdk)\end{array}\)
Vậy giá trị của phân thức \(\dfrac{{{x^2} - 1}}{{{x^2} + 2x + 1}}\) bằng \(0\) khi \(x = 1\).
Tìm \(x\) biết \(\left( {x-32} \right):16 = 48\).
Ta có:
\(\begin{array}{l}\left( {x-32} \right):16 = 48\\x - 32 = 48 \times 16\\x - 32 = 768\\x = 768 + 32\\x = 800\end{array}\).
Con hãy tìm trong đoạn văn tiếng chứa vần ông ?

Chạy
chán,
mèo
con
lại
nép
vào
một
gốc
cau,
một
sợi
lông
cũng
không
động:
nó
rình
một
con
bướm
đang
chợp
chờn
bay
qua.
Bỗng
cái
đuôi
quất
mạnh
một
cái,
mèo
con
chồm
ra.
Chạy
chán,
mèo
con
lại
nép
vào
một
gốc
cau,
một
sợi
lông
cũng
không
động:
nó
rình
một
con
bướm
đang
chợp
chờn
bay
qua.
Bỗng
cái
đuôi
quất
mạnh
một
cái,
mèo
con
chồm
ra.
Đáp án đúng là:
Chạy chán, mèo con lại nép vào một gốc cau, một sợi lông cũng không động: nó rình một con bướm đang chợp chờn bay qua. Bỗng cái đuôi quất mạnh một cái, mèo con chồm ra.
Hình lập phương có thể tích \(512c{m^3}\) thì có diện tích toàn phần là:
Ta có: \(8. 8. 8 = 512\) nên độ dài hình lập phương đã cho có cạnh là \(8cm\).
Diện tích toàn phần của hình lập phương đã cho là: \(8 \times 8 \times 6 = 384\,\,(c{m^2})\).
Vậy hình lập phương có thể tích \(512c{m^3}\) thì có diện tích toàn phần là \(384c{m^2}\).
Số câu đúng trong các câu sau là:
1/ Số \(0\) là số tự nhiên nhỏ nhất.
2/ Số \(100\) là số tự nhiên lớn nhất.
3/ Ba điểm thẳng hàng là ba điểm cùng thuộc 1 đường thẳng.
4/ Qua 3 điểm không thẳng hàng ta vẽ được nhiều nhất 3 đường thẳng phân biệt.
Các khẳng định đúng là:
1/ Số \(0\) là số tự nhiên nhỏ nhất vì tập hợp số tự nhiên là \(\mathbb{N} = \left\{ {0;1;2;...} \right\}\).
3/ Ba điểm thẳng hàng là ba điểm cùng thuộc 1 đường thẳng.
4/ Qua 3 điểm không thẳng hàng ta vẽ được nhiều nhất 3 đường thẳng phân biệt. Chằng hạn với ba điểm \(A,B,C\) phân biệt không thẳng hàng ta vẽ được các đường thẳng \(AB,BC,AC.\)
Khẳng định sai là:
2/ Số \(100\) là số tự nhiên lớn nhất vì có rất nhiều số tự nhiên lớn hơn \(100\) chẳng hạn như \(101;102;...\)
Vậy có ba khẳng định đúng.
Con hãy tìm trong đoạn văn tiếng chứa vần uôi ?

Mèo
con
chạy
giỡn
hết
góc
này
đến
góc
khác,
hai
tai
dựng
đứng
lên,
cái
đuôi
ngoe
nguẩy.
Chạy
chán,
mèo
con
lại
nép
vào
một
gốc
cau,
một
sợi
lông
cũng
không
động:
nó
rình
một
con
bướm
đang
chợp
chờn
bay
qua.
Bỗng
cái
đuôi
quất
mạnh
một
cái,
mèo
con
chồm
ra.
Mèo
con
chạy
giỡn
hết
góc
này
đến
góc
khác,
hai
tai
dựng
đứng
lên,
cái
đuôi
ngoe
nguẩy.
Chạy
chán,
mèo
con
lại
nép
vào
một
gốc
cau,
một
sợi
lông
cũng
không
động:
nó
rình
một
con
bướm
đang
chợp
chờn
bay
qua.
Bỗng
cái
đuôi
quất
mạnh
một
cái,
mèo
con
chồm
ra.
Đáp án đúng là:
Mèo con chạy giỡn hết góc này đến góc khác, hai tai dựng đứng lên, cái đuôi ngoe nguẩy. Chạy chán, mèo con lại nép vào một gốc cau, một sợi lông cũng không động: nó rình một con bướm đang chợp chờn bay qua. Bỗng cái đuôi quất mạnh một cái, mèo con chồm ra.
Cho hình vẽ sau: biết \(EF//BC\). Tìm đáp án sai trong các đáp án sau:
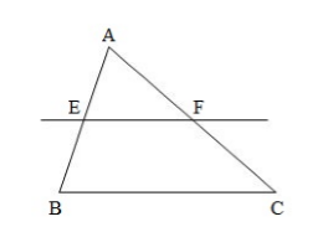
Ta có: \(EF//BC\) nên ta có các tỉ lệ thức đúng là:
\(\dfrac{{AE}}{{AB}} = \dfrac{{AF}}{{AC}};\,\,\dfrac{{AE}}{{EB}} = \dfrac{{AF}}{{FC}};\,\,\dfrac{{BC}}{{EF}} = \dfrac{{AC}}{{AF}};\,\,\dfrac{{EF}}{{BC}} = \dfrac{{AE}}{{AB}}\)
Đáp án sai là: \(\dfrac{{EF}}{{BC}} = \dfrac{{AE}}{{EB}}\)
Từ trái nghĩa với từ “cao” là:

c. thấp
c. thấp
c. thấp
Trái nghĩa với cao là thấp.
=> Đáp án: c
Tập nghiệm của phương trình \(\dfrac{2}{{x + 1}} + \dfrac{1}{{2 - x}} = \dfrac{{3x - 11}}{{(x + 1)(x - 2)}}\) là:
TXĐ: \(x \ne - 1;x \ne 2\)
Ta có: \(\dfrac{2}{{x + 1}} + \dfrac{1}{{2 - x}} = \dfrac{{3x - 11}}{{(x + 1)(x - 2)}} \)\(\Leftrightarrow \dfrac{2}{{x + 1}} - \dfrac{1}{{x - 2}} = \dfrac{{3x - 11}}{{(x + 1)(x - 2)}}\)
\( \Rightarrow 2(x - 2) - (x + 1) = 3x - 11\)
\( \Leftrightarrow 2x - 4 - x - 1 = 3x - 11\)
\( \Leftrightarrow x = 3\left( {tm} \right)\)
Vậy phương trình có nghiệm duy nhất \(x = 3.\)
Một hình tròn có chu vi là \(50,24cm.\) Tìm bán kính của hình tròn đó.
Bán kính hình tròn bằng: \(50,24:2:3,14 = 8\,cm\).
Số nghiệm của phương trình \(\left| {2x + 3} \right| - 5 = 0\) là:
\(\left| {2x + 3} \right| - 5 = 0 \Leftrightarrow \left| {2x + 3} \right| = 5\)
\( \Leftrightarrow \left[ \begin{array}{l}2x + 3 = 5\\2x + 3 = - 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 4\end{array} \right.\)
Vậy tập nghiệm của phương trình là \(S = \left\{ {1; - 4} \right\}\).
Hay phương trình đã cho có 2 nghiệm.
Tổng của hai số là \(25.\) Tỉ số của hai số đó là \(\dfrac{2}{3}\). Tìm số bé.
Tỉ số của hai số là: \(\dfrac{2}{3}\) nên số bé chiếm \(2\) phần thì số lớn chiếm \(3\) phần.
Tổng số phần bằng nhau là \(2 + 3 = 5\) phần.
Số bé là: \(25:5 \times 2 = 10.\)
Tập nghiệm của bất phương trình \(\dfrac{{2x - 3}}{2} > \dfrac{{8x - 11}}{6}\) là:
Ta có: \(\dfrac{{2x - 3}}{2} > \dfrac{{8x - 11}}{6} \)\(\Leftrightarrow 3(2x - 3) > 8x - 11\)
\( \Leftrightarrow 6x - 9 > 8x - 11\)
\( \Leftrightarrow 2x < 2 \Leftrightarrow x < 1\)
Vậy tập nghiệm của bất phương trình là \(S = \left\{ {x\left| {x < 1} \right.} \right\}\).
Kết quả của phép tính \(29,32 + 41,57 + 27,25\) là:
Ta có:
\(29,32 + 41,57 + 27,25\)
\(\begin{array}{l} = 70,89 + 27,25\\ = 98,14\end{array}\).
Đoạn thơ sau sử dụng những dấu câu nào:
Một ngôi sao chẳng sáng đêm
Một thân lúa chín, chẳng nên mùa vàng
Một người - đâu phải nhân gian
Sống chăng, một đốm lửa tàn mà thôi !

dấu phẩy
dấu gạch ngang
dấu chấm than
dấu phẩy
dấu gạch ngang
dấu chấm than
dấu phẩy
dấu gạch ngang
dấu chấm than
Các dấu câu có trong đoạn thơ là:
b. dấu phẩy
c. dấu gạch ngang
d. dấu chấm than
Một đội sản xuất theo kế hoạch mỗi ngày phải trồng 300 cây xanh. Khi thực hiện, mỗi ngày đội đã trồng thêm được 100 cây xanh, do đó đội đã hoàn thành trước kế hoạch 1 ngày và còn trồng thêm được 600 cây xanh. Hỏi theo kế hoạch, đội sản xuất đó phải trồng bao nhiêu cây xanh?
Gọi số ngày đội phải trồng xong số cây xanh theo kế hoạch là \(x\) (cây) (ĐK: \(x > 1;x \in \mathbb{N}\))
\(\Rightarrow \)số cây đội phải trồng theo kế hoạch là: \(300x\) (cây)
Thực tế: Số ngày hoàn thành công việc là \(x - 1\) (ngày)
Số cây trồng được là: \(400\left( {x{\rm{ }} - 1} \right)\) (cây)
Vì thực tế số cây trồng được nhiều hơn kế hoạch là \(600\) cây nên ta có phương trình:
\(\begin{array}{l}400\left( {x - 1} \right)-300x = 600\\ \Leftrightarrow 400x - 400 - 300x = 600\\ \Leftrightarrow 100x = 1000\\ \Leftrightarrow x = 10\,\left( {tm} \right)\end{array}\)
Vậy số cây tổ phải trồng theo kế hoạch là: \(10.300 = 3000\) (cây).
Với giá trị nào của x thì giá trị của phân thức \(\dfrac{{3{\rm{x}} + 1}}{{x + 2}}\) nhỏ hơn \(2.\)
\(\dfrac{{3{\rm{x}} + 1}}{{x + 2}} < 2\)
ĐKXĐ: \(x \ne - 2\)
\(\begin{array}{l}\,\,\,\,\dfrac{{3{\rm{x}} + 1}}{{x + 2}} < 2\\ \Leftrightarrow \dfrac{{3{\rm{x}} + 1}}{{x + 2}} < \dfrac{{2.\left( {x + 2} \right)}}{{x + 2}} \\\Leftrightarrow \dfrac{{3{\rm{x}} + 1}}{{x + 2}} - \dfrac{{2{\rm{x}} + 4}}{{x + 2}} < 0\\ \Leftrightarrow \dfrac{{3{\rm{x}} + 1 - 2{\rm{x}} - 4}}{{x + 2}} < 0 \Leftrightarrow \dfrac{{x - 3}}{{x + 2}} < 0\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x - 3 < 0\\x + 2 > 0\end{array} \right.\\\left\{ \begin{array}{l}x - 3 > 0\\x + 2 < 0\end{array} \right.\end{array} \right. \\\Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x < 3\\x > - 2\end{array} \right.\\\left\{ \begin{array}{l}x > 3\\x < - 2\end{array} \right.(KTM)\end{array} \right.\\ \Leftrightarrow - 2 < x < 3\end{array}\)
Kết hợp ĐKXĐ thì \( - 2 < x < 3\) thỏa mãn.
Vậy để \(\dfrac{{3{\rm{x}} + 1}}{{x + 2}} < 2\) thì \( - 2 < x < 3.\)
Một trường Trung học Cơ sở có tất cả \(1268\) học sinh. Trong đó, số học sinh nam nhiều hơn số học sinh nữ \(126\) bạn. Hỏi trường đó có bao nhiêu học sinh nam?
Số học sinh nam của trường đó là:
\(\left( {1268 + 126} \right):2 = 697\) học sinh.
Một ô tô đi từ một trường THCS lúc \(7\) giờ sáng, dự kiến đến khu du lịch Khoang Xanh – Suối Tiên lúc \(8\) giờ \(24\) phút. Nhưng do trời mưa nên mỗi giờ ô tô đã đi chậm hơn dự kiến là \(9km\) nên đến \(8\) giờ \(45\) phút xe mới tới Khoang Xanh – Suối Tiên. Tính độ dài quãng đường từ trường THCS đến khu du lịch Khoang Xanh – Suối Tiên.
Gọi vận tốc dự kiến ô tô sẽ đi là \(x\,\,(km/h);\,\left( {x > 9} \right)\).
\( \Rightarrow \) Vận tốc thực tế của ô tô là \(x - 9\,\,(km/h)\).
Theo dự kiến, ô tô đi từ trường THCS đến khu du lịch Khoang Xanh – Suối Tiên hết thời gian là:
\(8\) giờ \(24\) phút \( - \,\,\,7\) giờ \( = 1\) giờ \(24\) phút \( = 1\dfrac{2}{5}\) giờ \( = \dfrac{7}{5}\) giờ.
Thực tế ô tô đi từ trường THCS đến khu du lịch Khoang Xanh – Suối Tiên hết thời gian là:
\(8\) giờ \(45\) phút \( - \,\,\,7\) giờ \( = 1\) giờ \(45\) phút \( = 1\dfrac{3}{4}\) giờ \( = \dfrac{7}{4}\) giờ
Theo bài ra ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,x.\dfrac{7}{5} = \left( {x - 9} \right).\dfrac{7}{4} \Leftrightarrow \dfrac{{7x. 4}}{{20}} = \dfrac{{\left( {x - 9} \right). 7. 5}}{{20}}\\ \Leftrightarrow 28x = \left( {x - 9} \right). 35 \Leftrightarrow 28x = 35x - 315\\ \Leftrightarrow 7x = 315 \Leftrightarrow x = 45\,(tm)\end{array}\).
Vậy vận tốc đi dự kiến của ô tô là \(63\,km/h\).
Độ dài quãng đường từ trường THCS đến khu du lịch Khoang Xanh – Suối Tiên là: \(45. \dfrac{7}{5} = 63\,\,(km).\)
Cho tam giác \(ABC\) cân tại \(A\) có \(AB = 10cm,\,\,BC = 12cm\), đường cao \(AH\). Gọi \(E,F\) lần lượt là hình chiếu của \(H\) trên \(AB\) và \(AC\). Gọi \(I\) là giao điểm của \(AH\) và \(EF\).
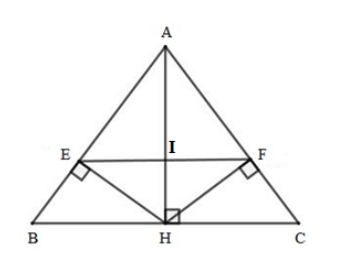
Chọn câu đúng.
*) Xét \(\Delta AEH\) và \(\Delta AHB\) có:
\(\begin{array}{l}+)\, \widehat H = \widehat E = {90^0}\\+) \,\widehat {EAH}\,\,\,chung\\ \Rightarrow \Delta AEH \backsim \Delta AHB\,\,\left( {g - g} \right)\end{array}\)
*) \(\Delta ABC\) cân tại \(A\) có: \(AH\) là đường cao nên \(AH\) đồng thời là đường trung tuyến, là đường phân giác của \(\Delta ABC\).
Xét hai tam giác vuông \(AEH\) và \(AFH\) có:
\(\widehat {EAH} = \widehat {FAH}\) (vì \(AH\) là tia phân giác của góc \(A\))
\(AH\) là cạnh chung
Vậy \(\Delta AEH = \Delta AFH\) (cạnh huyền – góc nhọn)
Suy ra: \(AE = AF\) (hai cạnh tương ứng)
Tam giác \(AEF\) cân (vì \(AE = AF\)) có: \(AI\) là đường phân giác nên \(AI\) đồng thời là đường cao
\( \Rightarrow AI \bot EF \Rightarrow AH \bot EF.\)
Lại có: \(AH \bot BC\), suy ra \(EF//BC\).

