Con lắc đơn - Các đại lượng đặc trưng - Viết phương trình dao động của con lắc đơn

\(\begin{array}{l}\ell  = (800 \pm 1)mm\\T = (1,78 \pm ,02)s\\T = 2\pi \sqrt {\frac{\ell }{g}}  \Rightarrow g = \frac{{4{\pi ^2}\ell }}{{{T^2}}} = \overline g  \pm \Delta g\\\overline g  = \frac{{4{\pi ^2}\overline \ell  }}{{{{\overline T }^2}}} = 9,968\\\frac{{\Delta g}}{g} = \frac{{\Delta l}}{{\overline l }} + 2\frac{{\Delta T}}{{\overline T }}\\\frac{{\Delta g}}{{\overline g }} = \frac{1}{{800}} + 2.\frac{{0,02}}{{1,78}} \Rightarrow \Delta g = 0,24\end{array}\)

Vậy g = 9,96 ± 0,24 m/s²

Ta có:

+ s₀ = 4cm

+ Tần số góc của con lắc:

\(\omega  = \sqrt {\frac{g}{l}}  = \sqrt {\frac{{10}}{1}}  = \sqrt {10}  = \pi \)

+ Tại t = 0:

\(\left\{ \begin{array}{l}s = {s_0}{\rm{cos}}\varphi  = 0\\v =  - \omega {s_0}\sin \varphi  > 0\end{array} \right. \to \varphi  =  - \frac{\pi }{2}\)

\(s = 4cos(\pi t - \frac{\pi }{2})cm\)

Ta có:

+ α₀ = 0,1 rad

+ Tần số góc của dao động:

\(\omega  = \frac{{2\pi }}{T} = 2\pi (ra{\rm{d}}/s)\)

Tại t=0:

\(\left\{ \begin{array}{l}\alpha  = {\alpha _0}{\rm{cos}}\varphi  = 0\\v =  - \omega {s_0}\sin \varphi  < 0\end{array} \right. \to \varphi  = \frac{\pi }{2}\)

\( \to \alpha  = 0,1c{\rm{os}}\left( {2\pi t + \frac{\pi }{2}} \right)\)

Ta có:

+ Tần số góc của dao động:

\(\omega  = \frac{{2\pi }}{T} = \pi (ra{\rm{d}}/s)\)

Mặt khác,

\(\omega  = \sqrt {\frac{g}{l}}  \to l = \frac{g}{{{\omega ^2}}} = \frac{{10}}{{{\pi ^2}}} \approx 1\)

+ Áp dụng hệ thức độc lập ta có:

\(s_0^2 = {s^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {(l\alpha )^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {(1.0,05)^2} + \frac{{0,{{157}^2}}}{{{\pi ^2}}} \to {s_0} = 0,07069m = 7,0693cm\)

Tại t=0:

\(\left\{ \begin{array}{l}s = {s_0}{\rm{cos}}\varphi  = 0,05\\v =  - \omega {s_0}\sin \varphi  > 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi {\rm{ = 0,7073}}\\\sin \varphi  < 0\end{array} \right. \to \varphi  \approx  - \frac{\pi }{4}\)

\( \to s = 7,069c{\rm{os}}\left( {\pi t - \frac{\pi }{4}} \right)cm\)

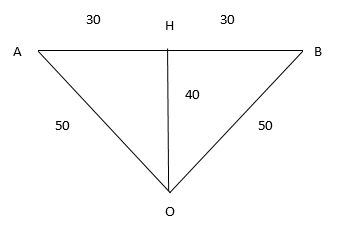
Coi hạt cườm như con lắc đơn dao động điều hòa có chiều dài dây treo là HO = 40 cm

\(\omega  = \sqrt {\dfrac{g}{l}}  = \sqrt {\dfrac{{10}}{{0,4}}}  = 5(rad/s)\)

Gần $4$ nhất nên chọn C

Ta có, lực kéo về cực đại: \({F_{kv\max }} = m{\omega ^2}s_o\)

\(\begin{array}{l}\left\{ \begin{array}{l}{F_{1\max }} = {m_1}{\omega ^2}s_0\\{F_{2\max }} = {m_2}{\omega ^2}s_0\end{array} \right.\\ \Rightarrow \dfrac{{{F_{1\max }}}}{{{F_{2\max }}}} = \dfrac{{{m_1}}}{{{m_2}}} = \dfrac{2}{3}\\ \Rightarrow \dfrac{{{m_1}}}{{1,2 - {m_1}}} = \dfrac{2}{3}\\ \Rightarrow {m_1} = 0,48kg = 480g\end{array}\)

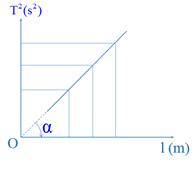
Ta có: \(T = 2\pi \sqrt {\dfrac{l}{g}}  \Rightarrow {T^2} = \dfrac{{4{\pi ^2}}}{g}l \Rightarrow \tan \alpha  = \dfrac{{4{\pi ^2}}}{g} \Rightarrow g = \dfrac{{4{\pi ^2}}}{{\tan \alpha }} = 9,76\) (m/s²)

+ Tần số góc : \(\omega  = \sqrt {\dfrac{g}{l}}  = \sqrt {\dfrac{{{\pi ^2}}}{1}}  = \pi \,\left( {rad/s} \right)\)

+ Ta có : \({\alpha _0} = {9^0} = \dfrac{{9\pi }}{{180}} = \dfrac{\pi }{{20}}\left( m \right) \Rightarrow {S_0} = {\alpha _0}.l = 5\pi \,\left( {cm\,} \right)\,\)

+ Tại t = 0 thì \(\alpha  =  - \dfrac{{{\alpha _0}}}{2} =  - 4,{5^0} \Rightarrow \varphi  =  \pm \dfrac{{2\pi }}{3}\)

Vật chuyển động chậm dần → ra biên \( \Rightarrow \varphi  =  + \dfrac{{2\pi }}{3}\)

Vậy phương trình dao động: \(s = 5\pi \cos \left( {\pi t + \dfrac{{2\pi }}{3}} \right)cm\)

Khi chiều dài con lắc là l, chu kì của con lắc là:

$T=\frac{\Delta t}{10}=2\pi \sqrt{\frac{l}{g}}\Rightarrow l=\frac{{{g}^{2}}.\Delta t}{{{10}^{2}}.4{{\pi }^{2}}}\,\,\left( 1 \right)$

Khi chiều dài của con lắc tăng thêm 36 cm, chu kì của con lắc là:

${T}'=\frac{\Delta t}{8}=2\pi \sqrt{\frac{l+0,36}{g}}\Rightarrow l+0,36=\frac{{{g}^{2}}.\Delta t}{{{8}^{2}}.4{{\pi }^{2}}}\left( 2 \right)$

Từ (1) và (2) ta có:

$\frac{l}{l+0,36}=\frac{{{8}^{2}}}{{{10}^{2}}}\Rightarrow l=0,64\,\,\left( m \right)=64\,\,\left( cm \right)$

Chu kì dao động: \(T = 2\pi \sqrt {\dfrac{l}{g}}  = 2\pi \sqrt {\dfrac{{0,5}}{{9,8}}}  = 1,42s\)

Biểu diễn các vị trí trên VTLG:

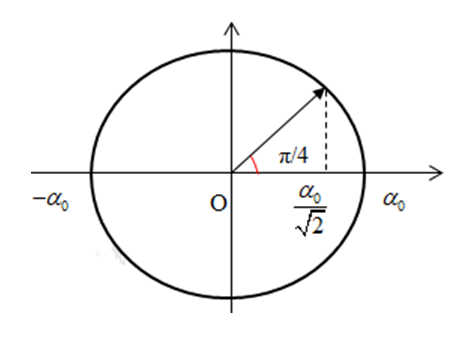
Từ VTLG ta thấy góc quét được là: \(\Delta \varphi  = \frac{\pi }{4}\)

\( \Rightarrow \) Thời gian ngắn nhất vật đi từ vị trí biên dương đến vị trí có li độ góc \(\alpha  = \dfrac{{{\alpha _0}}}{{\sqrt 2 }}\) là:

\(\Delta t = \frac{{\Delta \varphi }}{\omega } = \Delta \varphi .\frac{T}{{2\pi }} = \frac{\pi }{4}.\frac{T}{{2\pi }} = \frac{T}{8} = \frac{{1,42}}{8} = 1,774s\)

Ta có, chu kì dao động của con lắc đơn:

\(T = 2\pi \sqrt {\frac{l}{g}}\) \( \Rightarrow {T^2} \sim l\)

Khi con lắc có chiều dài \(l = {l_1} + {l_2}\) thì chu kì dao động khi đó:

\({T^2} = T_1^2 + T_2^2 = {1^2}\,\,\,\,\left( 1 \right)\)  

Khi con lắc có chiều dài \(l' = {l_2} - {l_1}\) thì chu kì dao động khi đó:

\(T{'^2} = T_2^2 - T_1^2 = 0,{53^2}\,\,\,\left( 2 \right)\)  

Từ (1) và (2) ta suy ra: \(\left\{ \begin{array}{l}{T_1} = 0,5996{\rm{s}}\\{T_2} = 0,8{\rm{s}}\end{array} \right.\)

+ Chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}}  = 2\pi \sqrt {\frac{{0,81}}{{9,87}}}  = 1,8s\)

+ \(\Delta t = 1,2s = \frac{{2T}}{3} = \frac{T}{2} + \frac{T}{6}\)

Vẽ trên trục ta được:

\( \Rightarrow \) Quãng đường vật đi được trong khoảng thời gian từ \(t = 0\) đến \(t = 1,2s\) là: \(S = 2{S_0} + \frac{{{S_0}}}{2} = \frac{{5{S_0}}}{2}\)

Lại có: \({S_0} = l{\alpha _0} = 0,81.\frac{{8\pi }}{{180}}\)

Ta suy ra: \(S = 0,28274m = 28,3cm\)

Con lắc đơn có quỹ đạo tròn, ở vị trí cân bằng, tổng hợp lực tác dụng lên con lắc bằng lực hướng tâm:

\({F_{ht}} = m{a_{ht}} = m\dfrac{{{v^2}}}{{\rm{l}}} \to \) A sai

Khi vật nặng ở vị trí biên, động năng của con lắc: \({W_d} = 0 \Rightarrow W = {W_t} \to \) B đúng

Dao động của con lắc là dao động điều hòa chỉ khi có biên độ nhỏ → C sai

Chuyển động của con lắc từ vị trí biên về vị trí cân bằng là nhanh dần → D sai