Các loại dao động

Mạch dao động duy trì sẽ cung cấp một phần năng lượng đúng bằng phần năng lượng mất mát trong mỗi giai đoạn (khi có I giảm) của mỗi chu kì

Công suất cần phải cung cấp thêm cho mạch để duy trì dao động được xác định bằng biểu thức: \(P = \frac{Q}{t} = {I^2}R = \frac{{I_0^2}}{2}R\)

Ta có: Cường độ dòng điện cực đại trong mạch: \({I_0} = {U_0}\sqrt {\frac{C}{L}}  = 5\sqrt {\frac{{{{8.10}^{ - 9}}}}{{{{2.10}^{ - 4}}}}}  = 0,01\sqrt {10} A\)

Công suất cần cung cấp để duy trì dao động của mạch: \(P = \frac{Q}{t} = \frac{{{I^2}Rt}}{t} = {I^2}R = \frac{{I_0^2}}{2}R \to R = \frac{{2P}}{{I_0^2}} = \frac{{{{2.6.10}^{ - 3}}}}{{{{\left( {0,01.\sqrt {10} } \right)}^2}}} = 12\Omega \)

Ta có:

Công suất cần cung cấp để duy trì dao động của mạch: \(P = \frac{Q}{t} = \frac{{{I^2}Rt}}{t} = {I^2}R = \frac{{I_0^2}}{2}R \to I_0^2 = \frac{{2P}}{R} = \frac{{2.18,{{75.10}^{ - 3}}}}{{15}} = 2,{5.10^{ - 3}} \to {I_0} = 0,05A\)

Cường độ dòng điện cực đại trong mạch: \(L{I_0}^2 = C{U_0}^2 \to {U_0} = {I_0}\sqrt {\frac{L}{C}}  = 0,05.\sqrt {\frac{{{{3.10}^{ - 6}}}}{{{{300.10}^{ - 12}}}}}  = 5V\)

Ta có: Cường độ dòng điện cực đại trong mạch: \({I_0} = {U_0}\sqrt {\frac{C}{L}}  = 10\sqrt {\frac{{{{18.10}^{ - 9}}}}{{3,{{6.10}^{ - 4}}}}}  = 0,05\sqrt 2 A\)

Công suất cần cung cấp để duy trì dao động của mạch: \(P = \frac{Q}{t} = \frac{{{I^2}Rt}}{t} = {I^2}R = \frac{{I_0^2}}{2}R \to R = \frac{{2P}}{{I_0^2}} = \frac{{{{2.6.10}^{ - 3}}}}{{{{\left( {0,05\sqrt 2 } \right)}^2}}} = 2,4\Omega \)

Cường độ dòng điện cực đại trong mạch: \({I_0} = {U_0}\sqrt {\frac{C}{L}}  = 5\sqrt {\frac{{{{2.10}^{ - 9}}}}{{{{20.10}^{ - 6}}}}}  = 0,05{\rm{A}}\)

Công suất cần cung cấp để duy trì dao động của mạch: \(P = \frac{Q}{t} = \frac{{{I^2}Rt}}{t} = {I^2}R = \frac{{I_0^2}}{2}R = \frac{{{{\left( {0,05} \right)}^2}}}{2}4 = {5.10^{ - 3}}{\rm{W}} = 5m{\rm{W}}\)

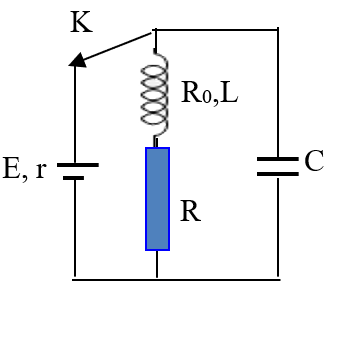
Khi K đóng \(I_0= \dfrac{E}{(R +r+R_0)} =\dfrac{12}{( 18+1+5)}=0,5A\)

Điện áp 2 đầu tụ C lúc đầu: \(U_0=I_0(R +R_0) = 0,5 .23=11,5V\)

Năng lượng lúc đầu của mạch: 

\(\begin{array}{l}W = \dfrac{{CU_0^2}}{2} + \dfrac{{LI_0^2}}{2} = \dfrac{{{{10}^{ - 4}}.11,5_{}^2}}{2} + \dfrac{{0,2.0,5_{}^2}}{2}\\ = {0,66125.10^{ - 2}} + 0,025 = 0,0316125J\end{array}\)

Năng lượng tỏa ra trên R và R₀  tỉ lệ thuận với điện trở.

\(\to \dfrac{R}{R_0}=\dfrac{18}{5}\)

\(\to\) Nhiệt lượng tỏa ra chia thành 23 phần thì tỏa trên R 18 phần.

Khi mạch tắt hoàn toàn thì năng lượng W chuyển thành nhiệt lượng tỏa ra trên

R và R₀  nên ta có: \(Q=W\)

\(\to\) Nhiệt lượng tỏa ra trên R: \(Q_R = \dfrac{{18}}{{23}}W = \dfrac{{18}}{{23}}.0,0316125 = 0,024740217J \approx 0,02474J=24,74 mJ\).

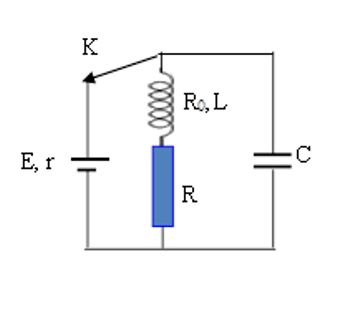
Cường độ dòng điện qua mạch trước khi mở khóa k

\({I_0} = \frac{E}{{R + {R_0} + r}} = \frac{{24}}{{24}} = 1{\rm{A}}\)

Điện áp giữa hai bản cực tụ điện \(U{\rm{ }} = {\rm{ }}I\left( {R{\rm{ }} + {\rm{ }}{R_0}} \right){\rm{ }} = {\rm{ }}23{\rm{ }}V\)

Năng lượng của mạch dao động sau khi ngắt khóa k

\({{\rm{W}}_0} = \frac{1}{2}L{I_0}^2 + \frac{1}{2}C{U^2} = 0,12645J = 126,45mJ\)

Trong thời gian từ khi ngắt khoá k đến khi dao động trong mạch tắt hoàn toàn. năng lượng này biến thành nhiệt lượng tỏa ra trên điện trở \(R\) và trên \({R_0}\) của cuộn dây.

Nhiệt lượng tỏa ra trên điện trở R là:   \({Q_R} = \frac{{{{\rm{W}}_0}}}{{R + {R_0}}}R = \frac{{126,45}}{{23}}18 = 98,96mJ\)

=> Chọn A

Cách 2:  

\(\begin{array}{l}{\rm{W}} = {{\rm{W}}_L} + {{\rm{W}}_C} = \frac{1}{2}.L{.1^2} + \frac{1}{2}.C.{\left( {24 - 1} \right)^2} = 0,12645J\\ =  > {Q_R} = \frac{R}{{R + {R_0}}}{\rm{W}} = \frac{{18}}{{23}}.0,12645 = 98,96mJ\end{array}\)   

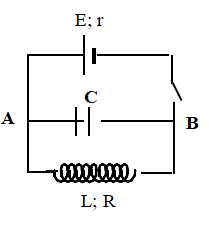
Khi dòng điện qua mạch ổn định (qua cuộn dây):

\(I = \frac{E}{{{r_n} + {r_d}}} = \frac{3}{5}(A)\)  ( Hay: I = E /(R + r) = 3/5 = 0,6 (A))

Hiệu điện thế ở hai đầu cuộn dây cũng chính là hiệu điện thế giữa 2 đầu tụ:

  U_AB = U₀ = IR = 1,8 (V)

Năng lượng dao động của mạch lúc ngắt nguồn: \(W = \frac{1}{2}L{I^2} + \frac{1}{2}C{U^2} = 4,{5.10^{ - 6}}(J)\)

Nhiệt lượng lớn nhất tỏa ra trên cuộn dây bằng (W )năng lượng dao động lúc đầu của mạch

Lúc đó nhiệt lượng lớn nhất toả ra trên cuộn dây bằng năng lượng của mạch khi đó

\({Q_{max}} = W = \frac{{CU_0^2}}{2} + \frac{{L{I^2}}}{2} = {\rm{ }}8,{1.10^{ - 6}} + {\rm{ }}0,{9.10^{ - 6}} = {\rm{ }}{9.10^{ - 6{\rm{ }}}}(J){\rm{ }} = {\rm{ }}9\mu J\)