Câu hỏi:
2 năm trước
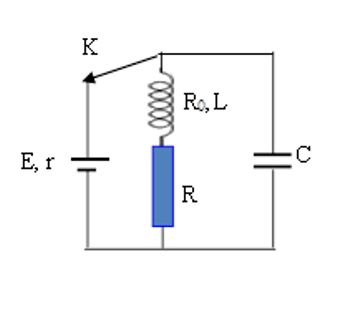
Cho mạch điện như hình vẽ, nguồn có suất điện động \(E = 24V,r = 1\Omega \) , tụ điện có điện dung \(C = 100\mu F\), cuộn dây có hệ số tự cảm \(L{\rm{ }} = {\rm{ }}0,2H\) và điện trở \({R_0} = 5\Omega \), điện trở \(R = 18\Omega \).Ban đầu khoá k đóng, khi trạng thái trong mạch đã ổn định người ta ngắt khoá k. Nhiệt lượng toả ra trên điện trở $R$ trong thời gian từ khi ngắt khoá k đến khi dao động trong mạch tắt hoàn toàn.
Trả lời bởi giáo viên
Đáp án đúng: a
Cường độ dòng điện qua mạch trước khi mở khóa k
\({I_0} = \frac{E}{{R + {R_0} + r}} = \frac{{24}}{{24}} = 1{\rm{A}}\)
Điện áp giữa hai bản cực tụ điện \(U{\rm{ }} = {\rm{ }}I\left( {R{\rm{ }} + {\rm{ }}{R_0}} \right){\rm{ }} = {\rm{ }}23{\rm{ }}V\)
Năng lượng của mạch dao động sau khi ngắt khóa k
\({{\rm{W}}_0} = \frac{1}{2}L{I_0}^2 + \frac{1}{2}C{U^2} = 0,12645J = 126,45mJ\)
Trong thời gian từ khi ngắt khoá k đến khi dao động trong mạch tắt hoàn toàn. năng lượng này biến thành nhiệt lượng tỏa ra trên điện trở \(R\) và trên \({R_0}\) của cuộn dây.
Nhiệt lượng tỏa ra trên điện trở R là: \({Q_R} = \frac{{{{\rm{W}}_0}}}{{R + {R_0}}}R = \frac{{126,45}}{{23}}18 = 98,96mJ\)
=> Chọn A
Cách 2:
\(\begin{array}{l}{\rm{W}} = {{\rm{W}}_L} + {{\rm{W}}_C} = \frac{1}{2}.L{.1^2} + \frac{1}{2}.C.{\left( {24 - 1} \right)^2} = 0,12645J\\ = > {Q_R} = \frac{R}{{R + {R_0}}}{\rm{W}} = \frac{{18}}{{23}}.0,12645 = 98,96mJ\end{array}\)
Hướng dẫn giải:
- Sử dụng định luật ohm: I = E /(R + r)
- Năng lượng của mạch dao động: \(W = \frac{1}{2}L{i^2} + \frac{1}{2}C{u^2}\)
Câu hỏi khác
- Bài tập mạch dao động LC các đại lượng đặc trưng có lời giải MÔN LÝ lớp 12
- Bài tập năng lượng của mạch dao động LC có lời giải MÔN LÝ lớp 12
- Bài tập phương trình dao động mạch LC q,u,i có lời giải MÔN LÝ lớp 12
- Bài tập điện từ trường - sóng điện từ lý 12 có lời giải
- Bài tập các loại dao động lý 12 có lời giải
