Góc $\widehat {BAH}$ bằng
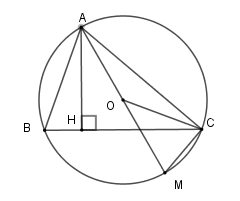
Xét \(\left( O \right)\) có \(\widehat {ABC}\) là góc nội tiếp chắn cung \(AC\) và \(\widehat {CAM}\) là góc nội tiếp chắn cung \(CM\)
Nên \(\widehat {ABC} = \dfrac{1}{2}\) số đo cung \(AC\) ; \(\widehat {CAM} = \dfrac{1}{2}\) số đo cung \(CM\)
Lại có số đo cung \(AC + \) số đo cung \(CM = 180^\circ \) nên \(\widehat {ABC} + \widehat {CAM} = \dfrac{{180^\circ }}{2} = 90^\circ \)
Mà \(\widehat {ABC} + \widehat {HAB} = 90^\circ \) nên \(\widehat {BAH} = \widehat {CAM}\) (1).
Lại có \(\Delta OAC\) cân tại \(O\) (do \(OA = OC = \) bán kính) nên \(\widehat {OCA} = \widehat {OAC}\) (2).
Từ (1) và (2) suy ra \(\widehat {OCA} = \widehat {BAH}\) .
Số đo góc $\widehat {ABM}$ là
Xét \(\left( O \right)\) có \(\widehat {ABM}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ABM} = 90^\circ \) .
Số đo góc $\widehat {ABM}$ là

Xét \(\left( O \right)\) có \(\widehat {ABM}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ABM} = 90^\circ \) .
Cho đường tròn $(O)$ và hai dây cung $AB,AC$ bằng nhau. Qua $A$ vẽ một cát tuyến cắt dây $BC$ ở $D$ và cắt $(O)$ ở $E$. Khi đó \(DA.DE\) bằng
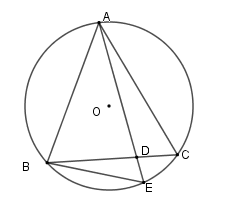
Xét \(\left( O \right)\) có \(\widehat {AEB} = \widehat {ABC}\) (hai góc nội tiếp chắn hai cung bằng nhau \(AB = AC\) )
Xét \(\Delta ADC\) và $\Delta BDE$ có \(\widehat {ADC} = \widehat {BDE}\) (đối đỉnh) và \(\widehat {AEB} = \widehat {ABC}\) (cmt) nên \(\Delta ADC\backsim\Delta BDE\left( {g - g} \right)\)\( \Rightarrow \dfrac{{AD}}{{BD}} = \dfrac{{DC}}{{DE}} \Rightarrow DA.DE = DB.DC\)
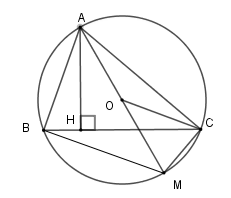
Gọi \(M\) là trung điểm \(BC\) . Chọn câu sai?
Tứ giác \(BHCF\) là hình bình hành (theo câu trước) có \(M\) là trung điểm của \(BC\) nên \(M\) cũng là trung điểm của \(HF\) hay \(HM = \dfrac{{HF}}{2}\)
Khi đó \(OM\) là đường trung bình của tam giác \(AHF\) nên \(AH//OM\).
Xét tam giác \(ABC\) có \(BD\) và \(CE\) là hai đường cao cắt nhau tại \(H\) nên \(H\) là trực tâm tam giác \(ABC \Rightarrow AH \bot BC\) mà \(AH//OM \Rightarrow OM \bot BC\) .
Đáp án D sai vì \(OM \bot BC\) mà \(BC\) cắt \(BF\) nên \(OM\) không thể vuông với \(BF.\)
Tích $DA.DC$ bằng
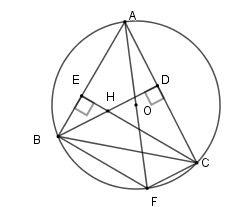
Xét hai tam giác vuông \(\Delta HDC\) và \(\Delta ADB\) có \(\widehat {EBH} = \widehat {ECA}\) (cùng phụ với \(\widehat {BAC}\) )
Nên $\Delta HDC\backsim\Delta ADB\left( {g - g} \right) \Rightarrow \dfrac{{DH}}{{DA}} = \dfrac{{DC}}{{DB}} \Rightarrow DH.DB = DA.DC$.
Chọn câu đúng?
Xét \(\left( O \right)\) có \(\widehat {ACF} = 90^\circ ;\widehat {ABF} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Suy ra \(CF \bot AC;BF \bot AB\) mà $BD \bot AC;CE \bot AB$\( \Rightarrow BD{\rm{//}}CF;CE{\rm{//}}BF\) $ \Rightarrow BHCF$ là hình bình hành
\( \Rightarrow BH = CF.\)
Chọn câu đúng?

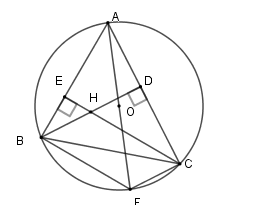
Xét \(\left( O \right)\) có \(\widehat {ACF} = 90^\circ ;\widehat {ABF} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Suy ra \(CF \bot AC;BF \bot AB\) mà $BD \bot AC;CE \bot AB$\( \Rightarrow BD{\rm{//}}CF;CE{\rm{//}}BF\) $ \Rightarrow BHCF$ là hình bình hành
\( \Rightarrow BH = CF.\)
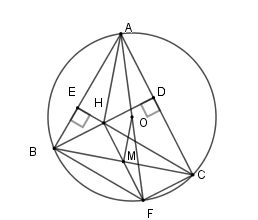
Gọi \(K\) là giao điểm của \(EB\) với \((O)\). Chọn khẳng định đúng?
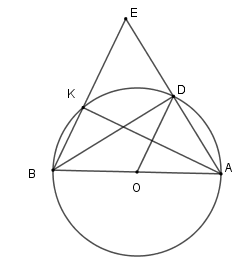
Xét \(\left( O \right)\) có $\widehat {BKA} = 90^\circ $ (góc nội tiếp chắn nửa đường tròn) nên \(AK \bot BE\)
Mà \(OD\) là đường trung bình của tam giác \(ABE\) nên \(OD{\rm{//}}EB\) từ đó \(BE = 2OD = 2R\) .
Góc \(AEB\) bằng bao nhiêu độ?
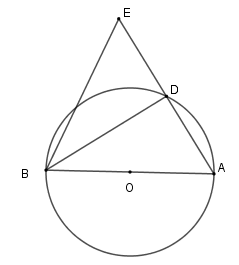
Xét \(\left( O \right)\) có $\widehat {BDA} = 90^\circ $ (góc nội tiếp chắn nửa đường tròn) nên \(BD \bot EA\) mà \(D\) là trung điểm \(EA\)
Nên \(\Delta BEA\) có \(BD\) vừa là đường cao vừa là đường trung tuyến nên \(\Delta BAE\) cân tại \(B\) .
Suy ra \(\widehat {BEA} = \widehat {BAD} = 50^\circ .\)
Góc \(AEB\) bằng bao nhiêu độ?

Xét \(\left( O \right)\) có $\widehat {BDA} = 90^\circ $ (góc nội tiếp chắn nửa đường tròn) nên \(BD \bot EA\) mà \(D\) là trung điểm \(EA\)
Nên \(\Delta BEA\) có \(BD\) vừa là đường cao vừa là đường trung tuyến nên \(\Delta BAE\) cân tại \(B\) .
Suy ra \(\widehat {BEA} = \widehat {BAD} = 50^\circ .\)
Cho tam giác $ABC$ có \(AB = 5cm;AC = 3cm\) đường cao $AH$ và nội tiếp trong đường tròn tâm $(O),$ đường kính $AD.$Khi đó tích $AH.AD$ bằng
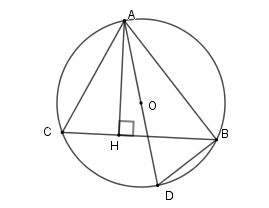
Xét \(\left( O \right)\) có \(\widehat {ACB} = \widehat {ADB}\) (hai góc nội tiếp cùng chắn cung \(AB\) ); \(\widehat {ABD} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Nên \(\Delta ACH \backsim \Delta ADB\left( {g - g} \right)\) $ \Rightarrow \dfrac{{AC}}{{AD}} = \dfrac{{AH}}{{AB}} \Rightarrow AH.AD = AC.AB$.
Suy ra \(AH.AD = 3.5 = 15c{m^2}\) .
Cho tam giác $ABC$ nội tiếp đường tròn $(O;R),$ đường cao $AH,$ biết $AB = 12{\rm{ }}cm,$$AC = 15{\rm{ }}cm,$ $AH = 6{\rm{ }}cm$.Tính đường kính của đường tròn $(O)$.
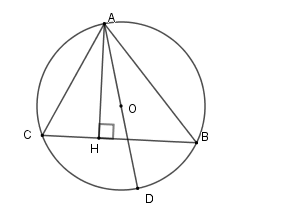
Kẻ đường kính \(AD\)
Xét \(\left( O \right)\) có \(\widehat {ACB} = \widehat {ADB}\) (hai góc nội tiếp cùng chắn cung \(AB\) ); \(\widehat {ABD} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Nên \(\Delta ACH \backsim \Delta ADB\left( {g - g} \right)\) $ \Rightarrow \dfrac{{AC}}{{AD}} = \dfrac{{AH}}{{AB}} \Rightarrow AH.AD = AC.AB$\( \Rightarrow AD = \dfrac{{AB.AC}}{{AH}} = \dfrac{{12.15}}{6} = 30\) .
Vậy đường kính của đường tròn là \(30cm\).
Cặp góc nào sau đây bằng nhau?
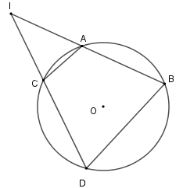
Xét \(\left( O \right)\) có \(\widehat {ACD}\) là góc nội tiếp chắn cung \(AD\) (chứa điểm \(B\) ); \(\widehat {ABD}\) là góc nội tiếp chắn cung $AD$ (chứa điểm \(C\) ) nên \(\widehat {ACD} + \widehat {ABD} = \dfrac{1}{2}.360^\circ = 180^\circ \)
Lại có \(\widehat {ACD} + \widehat {ACI} = 180^\circ \) nên \(\widehat {ACI} = \widehat {IBD}\) .
Tương tự ta có \(\widehat {IAC} = \widehat {IDB}\) .
Số đo $\widehat {ACM}$ là
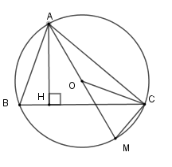
Xét \(\left( O \right)\) có \(\widehat {ACM}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ACM} = 90^\circ \) .
Hai đoạn thẳng nào sau đây bằng nhau?
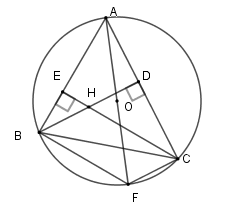
Xét \(\left( O \right)\) có \(\widehat {ACF} = 90^\circ ;\widehat {ABF} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Suy ra \(CF \bot AC;BF \bot AB\) mà $BD \bot AC;CE \bot AB$\( \Rightarrow BD{\rm{//}}CF;CE{\rm{//}}BF\)
$ \Rightarrow BHCF$ là hình bình hành
\( \Rightarrow BH = CF;BF = CH\) .
Tam giác $ABE$ là tam giác gì?
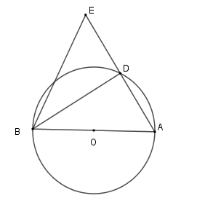
Xét \(\left( O \right)\) có $\widehat {BDA} = 90^\circ $ (góc nội tiếp chắn nửa đường tròn) nên \(BD \bot EA\) mà \(D\) là trung điểm \(EA\)
Nên \(\Delta BEA\) có \(BD\) vừa là đường cao vừa là đường trung tuyến nên \(\Delta BAE\) cân tại \(B\) .
Hình nào dưới đây biểu diễn góc nội tiếp?

Hình \(1\) góc \(\widehat {BOA}\) là góc ở tâm .
Hình \(3\) có \(1\) cạnh không phải là dây của đường tròn.
Hình \(4\) đỉnh $B$ không nằm trên đường tròn.
Hình \(2\) góc \(\widehat {BCA}\) là góc nội tiếp chắn cung \(AB\)
Góc nội tiếp nhỏ hơn hoặc bằng \(90^\circ \) có số đo
Trong một đường tròn:
Góc nội tiếp (nhỏ hơn hoặc bằng $90^\circ $) có số đo bằng nửa số đo góc ở tâm cùng chắn một cung.
Khẳng định nào sau đây là sai?
Trong một đường tròn:
+ Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
+ Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
+ Góc nội tiếp chắn nửa đường tròn là góc vuông.
Như vậy hai góc nội tiếp bằng nhau có thể cùng chắn một cung hoặc chắn các cung bằng nhau .
Phương án A, B, C đúng và D sai

