Câu hỏi:
2 năm trước
Cho tam giác $ABC$ nội tiếp đường tròn $(O;R),$ đường cao $AH,$ biết $AB = 12{\rm{ }}cm,$$AC = 15{\rm{ }}cm,$ $AH = 6{\rm{ }}cm$.Tính đường kính của đường tròn $(O)$.
Trả lời bởi giáo viên
Đáp án đúng: d
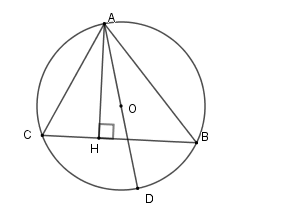
Kẻ đường kính \(AD\)
Xét \(\left( O \right)\) có \(\widehat {ACB} = \widehat {ADB}\) (hai góc nội tiếp cùng chắn cung \(AB\) ); \(\widehat {ABD} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Nên \(\Delta ACH \backsim \Delta ADB\left( {g - g} \right)\) $ \Rightarrow \dfrac{{AC}}{{AD}} = \dfrac{{AH}}{{AB}} \Rightarrow AH.AD = AC.AB$\( \Rightarrow AD = \dfrac{{AB.AC}}{{AH}} = \dfrac{{12.15}}{6} = 30\) .
Vậy đường kính của đường tròn là \(30cm\).
Hướng dẫn giải:
Sử dụng kết quả: Cho tam giác $ABC$ có đường cao $AH$ và nội tiếp trong đường tròn tâm $(O)$, đường kính $AD.$ Khi đó tích $AB.AC = AH.AD$ (đã được chứng minh ở các câu trước)
