Góc $\widehat {BAH}$ bằng

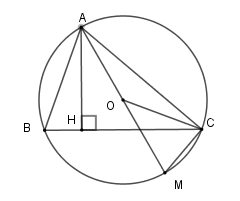
Xét $\left( O \right)$ có $\widehat {ABC}$ là góc nội tiếp chắn cung $AC$  và $\widehat {CAM}$ là góc nội tiếp chắn cung $CM$

Nên $\widehat {ABC} = \dfrac{1}{2}$ số đo cung $AC$ ; $\widehat {CAM} = \dfrac{1}{2}$ số đo cung $CM$

Lại có số đo cung $AC +$ số đo cung $CM = 180^\circ$  nên $\widehat {ABC} + \widehat {CAM} = \dfrac{{180^\circ }}{2} = 90^\circ$

Mà $\widehat {ABC} + \widehat {HAB} = 90^\circ$  nên  $\widehat {BAH} = \widehat {CAM}$  (1).

Lại có $\Delta OAC$ cân tại $O$ (do $OA = OC =$ bán kính) nên $\widehat {OCA} = \widehat {OAC}$ (2).

Từ (1) và (2) suy ra $\widehat {OCA} = \widehat {BAH}$ .