Trả lời bởi giáo viên
Đáp án đúng: a
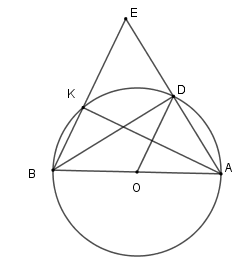
Xét \(\left( O \right)\) có $\widehat {BKA} = 90^\circ $ (góc nội tiếp chắn nửa đường tròn) nên \(AK \bot BE\)
Mà \(OD\) là đường trung bình của tam giác \(ABE\) nên \(OD{\rm{//}}EB\) từ đó \(BE = 2OD = 2R\) .
Hướng dẫn giải:
Sử dụng tính chất góc nội tiếp, tính chất đường trung bình và quan hệ từ vuông góc đến song song

