Hình hộp chữ nhật có số cạnh là:
Hình hộp chữ nhật có \(8\) đỉnh, \(6\) mặt và \(12\) cạnh.
Vậy hình hộp chữ nhật có \(12\) cạnh.
Có bao nhiêu đường thẳng được tạo thành từ \(6\) điểm phân biệt (không có ba điểm nào thẳng hàng)?
Gọi \(6\) điểm phân biệt là: \(A,B,C,D,E,F\)
Các đường thẳng tạo thành là: \(AB,AC,AD,AE,AF,BC,BD,BE,BF,\)\(CD,CE,CF,DE,DF,EF.\)
Vậy có \(15\) đường thẳng
Trong hình vẽ sau đây với \(MN//BC\) thì số đo \(x\) bằng:
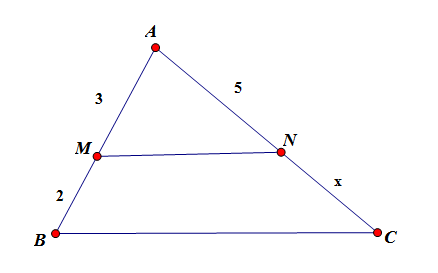
Áp dụng tính định lý Ta-lét ta có: \(MN//BC\) nên \(\dfrac{{AM}}{{MB}} = \dfrac{{AN}}{{NC}} \Rightarrow NC = \dfrac{{MB.AN}}{{AM}} = \dfrac{{2.5}}{3} = \dfrac{{10}}{3}\).
Vậy \(NC = \dfrac{{10}}{3}\).
Một khu vườn hình thang có đáy lớn là \(42m,\) đáy bé bằng \(\dfrac{2}{3}\) đáy lớn và chiều cao hơn đáy bé \(2m.\) Tính diện tích khu vườn hình thang đó?
Đáy bé của hình thang có độ dài là: \(\dfrac{2}{3} \times 42 = 28m\)
Chiều cao của hình thang có độ dài là: \(28 + 2 = 30m\)
Diện tích hình thang là: \(\dfrac{1}{2} \times \left( {42 + 28} \right) \times 30 = 1050\,{m^2}\)
Đáp số: \(1050\,{m^2}.\)
Cho \(\Delta DEF\) đồng dạng với \(\Delta ABC\) theo tỉ số đồng dạng \(k = \dfrac{1}{2}\) thì \(\dfrac{{{S_{DEF}}}}{{{S_{ABC}}}}\) bằng:
Do \(\Delta DEF \backsim \Delta ABC\) nên \(\dfrac{{{S_{DEF}}}}{{{S_{ABC}}}} = {\left( {\dfrac{{DE}}{{AB}}} \right)^2} = {k^2} = {\left( {\dfrac{1}{2}} \right)^2} = \dfrac{1}{4}\).
Vậy \(\dfrac{{{S_{DEF}}}}{{{S_{ABC}}}} = \dfrac{1}{4}\) .
Giá trị của \(x\) thỏa mãn \(x:\left[ {\left( {1800 + 600} \right):30} \right] = 560:\left( {315 - 35} \right)\) là:
Ta có:
\(\begin{array}{l}x:\left[ {\left( {1800 + 600} \right):30} \right] = 560:\left( {315 - 35} \right)\\x:\left( {2400:30} \right) = 560:280\\x:80 = 2\\x = 2 \times 80\\x = 160\end{array}\)
Phân tích đa thức \({x^2} - x - 6\) thành nhân tử được kết quả là:
\({x^2} - x - 6 = {x^2} - 3x + 2x - 6 = \left( {{x^2} - 3x} \right) + \left( {2x - 6} \right) = x\left( {x - 3} \right) + 2\left( {x - 3} \right) = \left( {x - 3} \right)\left( {x + 2} \right)\)
Một cửa hàng có \(7250kg\) gạo. Cửa hàng đã bán được \(\dfrac{2}{5}\) số gạo đó. Sau đó lại bán thêm 370kg gạo nữa. Hỏi cửa hàng còn lại bao nhiêu?
\(\dfrac{2}{5}\) số gạo ban đầu là: \(\dfrac{2}{5} \times 7250 = 2900kg\)
Số gạo còn lại sau khi bán \(\dfrac{2}{5}\) số gạo ban đầu là: \(7250 - 2900 = 4350kg\)
Số gạo còn lại sau khi bán thêm \(370kg\) gạo là: \(4350 - 370 = 3980kg\)
Đáp số: \(3980kg\)
Người ta muốn lót gạch một nền nhà hình chữ nhật có chu vi \(32m,\) có chiều rộng kém chiều dài \(4m;\) bằng những viên gạch vuông cạnh \(2dm.\) Tìm số gạch cần dùng.
Nửa chu vi hình chữ nhật là: \(32:2 = 16\,m\)
Suy ra tổng chiều dài và chiều rộng là \(16m,\) hiệu chiều dài và chiều rộng là \(4m\)
Chiều dài hình chữ nhật là: \(\left( {16 + 4} \right):2 = 10m\)
Chiều rộng hình chữ nhật là: \(10 - 4 = 6m\)
Diện tích hình chữ nhật là: \(10 \times 6 = 60{m^2}\)
Diện tích viên gạch là: \(2 \times 2 = 4\,d{m^2} = 0,04{m^2}\)
Số viên gạch cần dùng là: \(60:0,04 = 1500\) viên.
Đáp số: \(1500\) viên.
Nghiệm của phương trình \(3x + 2(x + 1) = 6x - 7\) là:
\(\begin{array}{l}3x + 2(x + 1) = 6x - 7\\ \Leftrightarrow 3x + 2x + 2 = 6x - 7\\ \Leftrightarrow 2 + 7 = 6x - 3x - 2x\\ \Leftrightarrow x = 9\end{array}\).
Vậy tập nghiệm của phương trình là \(S = {\rm{\{ 9\} }}{\rm{.}}\)
Một thửa ruộng hình thang có tổng độ dài hai đáy là 250m, chiều cao bằng \(\dfrac{3}{5}\) tổng độ dài hai đáy. Trung bình cứ \(100{m^2}\) của thửa ruộng đó thu được 64kg thóc. Hỏi trên cả thửa ruộng đó người ta thu được bao nhiêu tấn thóc?
Chiều cao của thửa ruộng hình thang là: \(250 \times \dfrac{3}{5} = 150\left( m \right)\)
Diện tích thửa ruộng hình thang là: \(250 \times 150:2 = 18750\left( {{m^2}} \right)\)
\(1m^2\) ruộng thu được số ki-lo-gam thóc là: \(64:100=0,64\,(kg)\)
Số ki-lô-gam thóc thu được trên cả thửa ruộng là: \(18750\times 0,64 = 12000\left( {kg} \right)\)
Đổi: \(12000kg = 12\) (tấn)
Phương trình \(\dfrac{5}{{x + 1}} + \dfrac{{2x}}{{(x + 1)(x - 4)}} = \dfrac{2}{{x - 4}}\) có tập nghiệm là:
ĐKXĐ: \(x \ne - 1;\,\,x \ne 4\)
\(\dfrac{5}{{x + 1}} + \dfrac{{2x}}{{(x + 1)(x - 4)}} = \dfrac{2}{{x - 4}}\)\( \Leftrightarrow \dfrac{{5(x - 4)}}{{(x + 1)(x - 4)}} + \dfrac{{2x}}{{(x + 1)(x - 4)}} = \dfrac{{2(x + 1)}}{{(x + 1)(x - 4)}}\)\( \Rightarrow 5(x - 4) + 2x = 2(x + 1)\\ \Leftrightarrow 5x - 20 + 2x = 2x + 2\)\( \Leftrightarrow 5x + 2x - 2x = 2 + 20\)\( \Leftrightarrow 5x = 22\)\(\Leftrightarrow x = \dfrac{{22}}{5}\,\,\,\left( {tm} \right).\)
Vậy tập nghiệm của phương trình là \(S = \left\{ {\dfrac{{22}}{5}} \right\}.\)
Hai kho A và B đều chứa hạt cà phê, biết khối lượng cà phê ở kho A bằng \(\dfrac{3}{5}\) khối
lượng cà phê ở kho B. Nếu chuyển 7 tấn cà phê từ kho A sang kho B thì kho A có khối lượng cà phê bằng \(\dfrac{4}{9}\) khối lượng cà phê ở kho B. Hỏi cả hai kho chứa bao nhiêu tấn cà phê?
\(7\) tấn cà phê của kho \(A\) ứng với phân số là: \(\dfrac{3}{5} - \dfrac{4}{9} = \dfrac{7}{{45}}\)
Số cà phê của kho A là: \(7:\dfrac{7}{{45}} = 45\) tấn.
Số cà phê của kho B ban đầu là: \(\dfrac{3}{5} \times 45 = 27\) tấn.
Cả hai kho chứa số tấn cà phê là: \(45 + 27 = 72\) tấn.
Đáp số: \(72\) tấn.
Biểu diễn tập nghiệm của bất phương trình \(7x + 4 \ge 5x - 8\) trên trục số ta được:
\(\begin{array}{l}7x + 4 \ge 5x - 8\\ \Leftrightarrow 7x - 5x \ge - 8 - 4\\ \Leftrightarrow 2x \ge - 12\\ \Leftrightarrow x \ge - 6\end{array}\).
Vậy tập hợp nghiệm của bất phương trình là \(S = {\rm{\{ }}x\,{\rm{| }}x \ge - 6{\rm{\} }}\).
Biểu diễn tập hợp nghiệm trên trục số:

Cho dãy số: \(3;18;48;93;153; \ldots ..\) Số \(11703\) là số hạng thứ bao nhiêu của dãy.
Ta thấy:
\(\begin{array}{l}18 = 3 + 15 \times 1\\48 = 18 + 15 \times 2\\93 = 48 + 15 \times 3\\...\end{array}\)
Từ dãy số ta phá hiện ra qui luật của dãy là: Số liền sau bằng số liền trước cộng với tích của \(15\) với số thứ tự của số liền trước trong dãy.
Gọi \(n\) là số thứ tự của số hạng \(11703,\) ta có:
\(3 + 15 \times 1 + 15 \times 2 + 15 \times 3 + ... + \left( {n - 1} \right) \times 15 = 11703\)
\(15 \times \left[ {1 + 2 + 3 + 4 + 5 + ... + \left( {n - 1} \right)} \right] = 11700\)
\(\begin{array}{l}15 \times \dfrac{{n - 1}}{2} \times n = 1170\\\left( {n - 1} \right) \times n = 1560\\\left( {n - 1} \right) \times n = 39 \times 40\end{array}\)
Suy ra: \(n = 40.\)
Số \(11703\) là số hạng thứ \(40\) trong dãy.
Một người đi xe ô tô từ A đến B với vận tốc 60 km/h. Đến B người đó làm việc trong 1 giờ 30 phút rồi quay về A với vận tốc 45km/h. Biết thời gian tổng cộng hết 6 giờ 24 phút. Tính quãng đường AB.
Gọi quãng đường AB dài \(x\,\left( {km} \right),\,\left( {x > 0} \right)\).
Thời gian người đó đi từ A đến B là \(\dfrac{x}{{60}}\,\left( h \right)\).
Thời gian người đó đi từ B đến A là \(\dfrac{x}{{45}}\,\,\left( h \right)\).
Đổi: 6 giờ 24 phút = 6,4h; 1 giờ 30 phút = 1,5h
Theo bài ta lập được phương trình sau:
\(\begin{array}{l}\,\,\,\,\,\,\,\dfrac{x}{{60}} + 1,5 + \dfrac{x}{{45}} = 6,4\\ \Leftrightarrow \dfrac{{3x}}{{60.3}} + \dfrac{{1,5.180}}{{180}} + \dfrac{{4x}}{{45.4}} = \dfrac{{6,4.180}}{{180}}\\ \Leftrightarrow 3x + 270 + 4x = 1152\\ \Leftrightarrow 7x + 270 - 1152 = 0 \Leftrightarrow x = 126\,\,\left( {tm} \right)\end{array}\).
Vậy quãng đường AB dài 126km.
Cho tam giác ABC vuông tại A. Kẻ đường cao AH (\(H \in BC\)), đường phân giác BD của góc ABC cắt AH tại E (\(E \in AH\)) và cắt AC tại D (\(D \in AC\)).
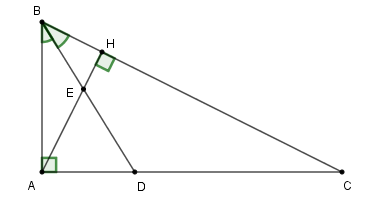
Hệ thức nào dưới đây là đúng?
Xét tam giác HBA và tam giác ABC ta có:
\(\begin{array}{l}\widehat {AHB} = \widehat {CAB} = {90^0}\,\,\left( {gt} \right)\\\widehat B\,\,\,chung\\ \Rightarrow \Delta HBA \backsim \Delta ABC\;(g - g)\\ \Rightarrow \dfrac{{BA}}{{BC}} = \dfrac{{BH}}{{BA}} \Leftrightarrow B{A^2} = BH.BC\,.\end{array}\).
Cho tam giác ABC vuông tại A. Kẻ đường cao AH (\(H \in BC\)), đường phân giác BD của góc ABC cắt AH tại E (\(E \in AH\)) và cắt AC tại D (\(D \in AC\)).

Biết \(AB = 12cm,AC = 16cm.\) Tính \(AD.\)
Áp dụng định lý Pitago cho tam giác vuông ABC ta có:
\(B{C^2} = A{B^2} + A{C^2} = {12^2} + {16^2} = 400 \Rightarrow BC = 20cm\)
Ta có: BD là phân giác góc B của tam giác ABC. Áp dụng tính chất đường phân giác của tam giác ta có tỉ lệ thức sau:
\(\begin{array}{l}\dfrac{{DC}}{{BC}} = \dfrac{{DA}}{{BA}} = \dfrac{{DC + DA}}{{BC + BA}} = \dfrac{{AC}}{{BC + BA}} = \dfrac{{16}}{{32}} = \dfrac{1}{2}\\ \Rightarrow \dfrac{{DA}}{{12}} = \dfrac{1}{2} \Leftrightarrow DA = \dfrac{{12}}{2} = 6cm\end{array}\).
Cho tam giác ABC vuông tại A. Kẻ đường cao AH (\(H \in BC\)), đường phân giác BD của góc ABC cắt AH tại E (\(E \in AH\)) và cắt AC tại D (\(D \in AC\)).

Chọn đáp án đúng nhất?
Ta có: \(\Delta HBA \backsim \Delta ABC\) (theo câu trước)
\( \Rightarrow \widehat {BAH} = \widehat {BCA}\;\,hay\,\widehat {BAE} = \widehat {BCD}\) (hai góc tương ứng)
Xét tam giác EAB và tam giác DCB ta có:
\(\begin{array}{l}\widehat {ABE} = \widehat {CBD}\;(gt)\\\widehat {BAE} = \widehat {BCD}\\ \Rightarrow \Delta E{\rm{A}}B \backsim \Delta DCB\; (g - g)\\ \Rightarrow \dfrac{{BE}}{{B{\rm{D}}}} = \dfrac{{BA}}{{BC}}\;\;(1)\end{array}\)
Ta lại có: \(\dfrac{{DA}}{{DC}} = \dfrac{{BA}}{{B{\rm{C}}}}\) (tính chất đường phân giác) (2)
Từ (1) và (2) suy ra: \(\dfrac{{DA}}{{DC}} = \dfrac{{BE}}{{B{\rm{D}}}}\).
Cho 3 số thực \(x, y, z\) thỏa mãn \(2x + 2y + z = 4.\)
Tìm giá trị lớn nhất của biểu thức: \(A = 2xy + yz + zx.\;\;\)
Ta có: \(2x + 2y + z = 4 \Leftrightarrow z = 4 - 2x - 2y.\)
\( \Rightarrow A = 2xy + yz + zx\)\( = 2xy + y\left( {4-2x-2y} \right) + x\left( {4-2x-2y} \right)\)\( = {\rm{ }}2xy + 4y-2xy-2{y^2} + 4x-2{x^2}-2xy\)\(= -2{x^2}-2xy + 4x-2{y^2} + 4y\)\( = - \left[ {\left( {{x^2} + 2xy + {y^2}} \right) - \dfrac{8}{3}\left( {x + y} \right) + \dfrac{{16}}{9}} \right] - \left( {{x^2} - \dfrac{4}{3}x + \dfrac{4}{9}} \right) - \left( {{y^2} - \dfrac{4}{3}y + \dfrac{4}{9}} \right) + \dfrac{8}{3}\)\(= - {\left( {x + y - \dfrac{4}{3}} \right)^2} - {\left( {x - \dfrac{2}{3}} \right)^2} - {\left( {y - \dfrac{2}{3}} \right)^2}+ \dfrac{8}{3}\)
Mà: \({\left( {x + y - \dfrac{4}{3}} \right)^2} \ge 0;\;{\left( {x - \dfrac{2}{3}} \right)^2} \ge 0;\;{\left( {y - \dfrac{2}{3}} \right)^2} \ge 0\) với mọi \(x,\;y\)
\( \Rightarrow A = - {\left( {x + y - \dfrac{4}{3}} \right)^2} - {\left( {x - \dfrac{2}{3}} \right)^2} - {\left( {y - \dfrac{2}{3}} \right)^2} + \dfrac{8}{3} \le \dfrac{8}{3}\) với mọi \( x,\;y\).
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}x + y - \dfrac{4}{3} = 0\\x - \dfrac{2}{3} = 0\\y - \dfrac{2}{3} = 0\end{array} \right. \Leftrightarrow x = y = \dfrac{2}{3}.\)
Vậy Amax = \(\dfrac{8}{3}\) khi \(\left\{ \begin{array}{l}x = y = \dfrac{2}{3}\\z = \dfrac{4}{3}\end{array} \right.\).