Câu hỏi:
2 năm trước
Cho tam giác ABC vuông tại A. Kẻ đường cao AH (\(H \in BC\)), đường phân giác BD của góc ABC cắt AH tại E (\(E \in AH\)) và cắt AC tại D (\(D \in AC\)).
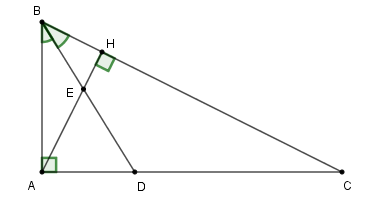
Hệ thức nào dưới đây là đúng?
Trả lời bởi giáo viên
Đáp án đúng: a
Xét tam giác HBA và tam giác ABC ta có:
\(\begin{array}{l}\widehat {AHB} = \widehat {CAB} = {90^0}\,\,\left( {gt} \right)\\\widehat B\,\,\,chung\\ \Rightarrow \Delta HBA \backsim \Delta ABC\;(g - g)\\ \Rightarrow \dfrac{{BA}}{{BC}} = \dfrac{{BH}}{{BA}} \Leftrightarrow B{A^2} = BH.BC\,.\end{array}\).
Hướng dẫn giải:
Chứng minh cặp tam giác đồng dạng theo trường hợp góc – góc. Suy ra hệ thức đúng về cạnh.
Câu hỏi khác
- Đề thi khảo sát chất lượng đầu năm - Đề số 1 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 2 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 4 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 5 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 3 toán 9 có lời giải
