Câu hỏi:
2 năm trước
Cho tam giác ABC vuông tại A. Kẻ đường cao AH (\(H \in BC\)), đường phân giác BD của góc ABC cắt AH tại E (\(E \in AH\)) và cắt AC tại D (\(D \in AC\)).
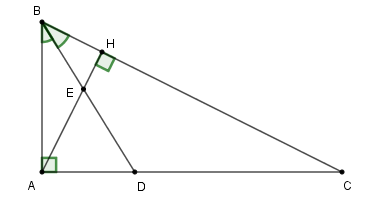
Biết \(AB = 12cm,AC = 16cm.\) Tính \(AD.\)
Trả lời bởi giáo viên
Đáp án đúng: a
Áp dụng định lý Pitago cho tam giác vuông ABC ta có:
\(B{C^2} = A{B^2} + A{C^2} = {12^2} + {16^2} = 400 \Rightarrow BC = 20cm\)
Ta có: BD là phân giác góc B của tam giác ABC. Áp dụng tính chất đường phân giác của tam giác ta có tỉ lệ thức sau:
\(\begin{array}{l}\dfrac{{DC}}{{BC}} = \dfrac{{DA}}{{BA}} = \dfrac{{DC + DA}}{{BC + BA}} = \dfrac{{AC}}{{BC + BA}} = \dfrac{{16}}{{32}} = \dfrac{1}{2}\\ \Rightarrow \dfrac{{DA}}{{12}} = \dfrac{1}{2} \Leftrightarrow DA = \dfrac{{12}}{2} = 6cm\end{array}\).
Hướng dẫn giải:
Áp dụng định lý Pitago và tính chất đường phân giác của tam giác để tính độ dài AD.
Chú ý: Đường phân giác của tam giác chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề góc đó.
Câu hỏi khác
- Đề thi khảo sát chất lượng đầu năm - Đề số 1 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 2 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 4 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 5 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 3 toán 9 có lời giải
