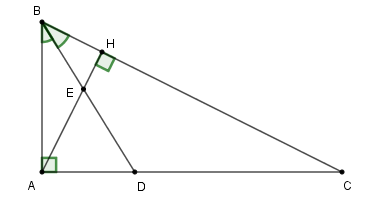
Cho tam giác ABC vuông tại A. Kẻ đường cao AH (\(H \in BC\)), đường phân giác BD của góc ABC cắt AH tại E (\(E \in AH\)) và cắt AC tại D (\(D \in AC\)).

Chọn đáp án đúng nhất?

Ta có: \(\Delta HBA \backsim \Delta ABC\) (theo câu trước)

\( \Rightarrow \widehat {BAH} = \widehat {BCA}\;\,hay\,\widehat {BAE} = \widehat {BCD}\) (hai góc tương ứng)

Xét tam giác EAB và tam giác DCB ta có:

\(\begin{array}{l}\widehat {ABE} = \widehat {CBD}\;(gt)\\\widehat {BAE} = \widehat {BCD}\\ \Rightarrow \Delta E{\rm{A}}B \backsim \Delta DCB\; (g - g)\\ \Rightarrow \dfrac{{BE}}{{B{\rm{D}}}} = \dfrac{{BA}}{{BC}}\;\;(1)\end{array}\)

Ta lại có: \(\dfrac{{DA}}{{DC}} = \dfrac{{BA}}{{B{\rm{C}}}}\) (tính chất đường phân giác) (2)

Từ (1) và (2) suy ra: \(\dfrac{{DA}}{{DC}} = \dfrac{{BE}}{{B{\rm{D}}}}\).