Hoạt động 1
Một vât dịch chuyển từ A đến B và tiếp tục dịch chuyển từ B đến C (Hình 49).
a) Biểu diễn vecto dịch chuyển của vật từ A đến B và từ B đến C.
b) Xác định vecto dịch chuyển tổng hợp của vật
Lời giải chi tiết:
a) vecto dịch chuyển của vật từ A đến B là \(\overrightarrow {AB} \)và từ B đến C là \(\overrightarrow {BC} \)
b) Tóm lại vật đó dịch chuyển từ A đến C, vecto dịch chuyển tổng hợp của vật là \(\overrightarrow {AC} \)
Hoạt động 2
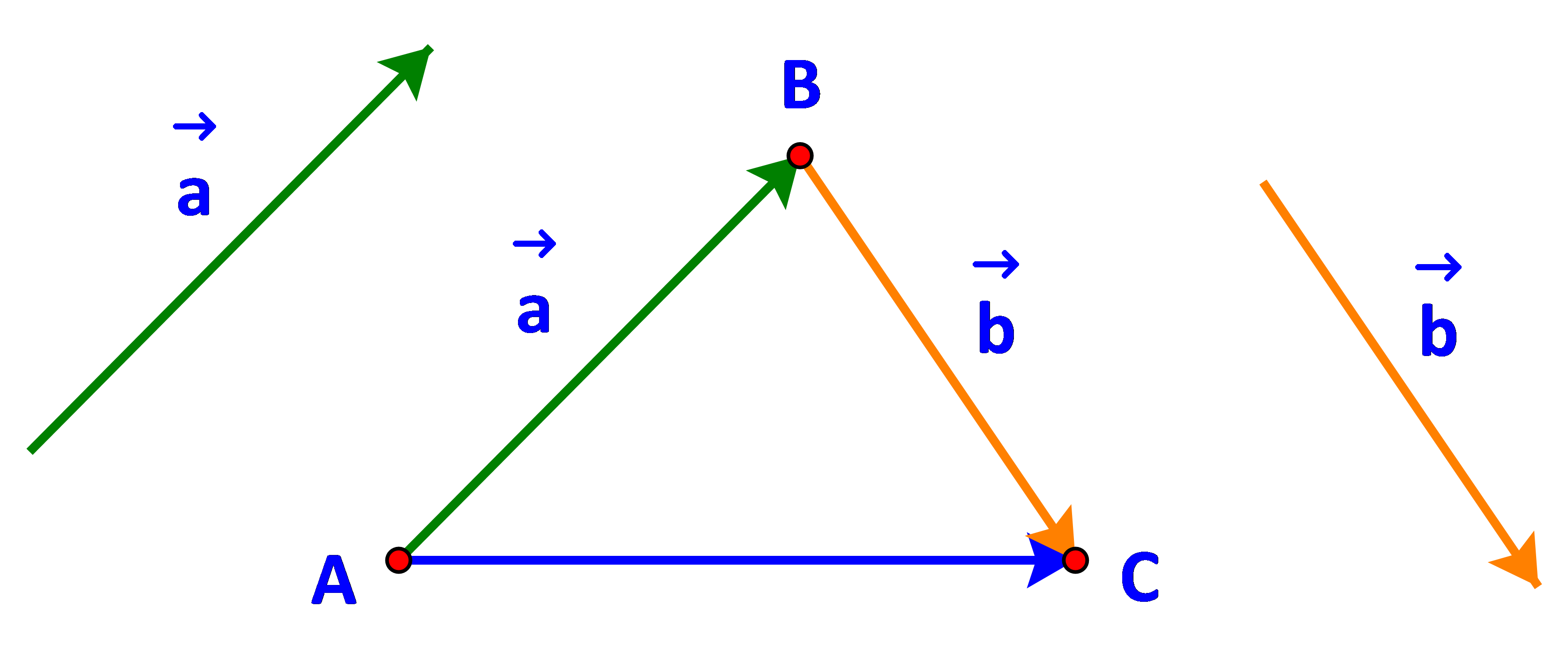
Cho hai vecto \(\overrightarrow a ,\overrightarrow b \). Lấy một điểm A tùy ý.
a) Vẽ \(\overrightarrow {AB} = a\), \(\overrightarrow {BC} = b\)
b) Tổng của hai vecto \(\overrightarrow a \) và \(\overrightarrow b \)bằng vecto nào?
Phương pháp giải:
a) Nêu cách xác định điểm B, điểm C.
b) Xác định tổng của hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \)
Lời giải chi tiết:
a) Gọi M, N lần lượt là điểm đầu và điểm cuối của vecto \(\overrightarrow a \).
Vì \(\overrightarrow a = \overrightarrow {AB} \Leftrightarrow \overrightarrow {MN} = \overrightarrow {AB} \) nên tứ giác MNBA là hình bình hành.
Nói cách khác B là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow a \) và điểm A.
Tương tự, C là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow b \) và điểm B.
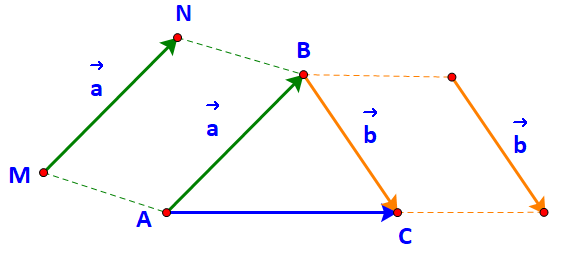
b) Dễ thấy: tổng của hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) là vecto \(\overrightarrow {AC} \).
Do đó tổng của hai vecto \(\overrightarrow a \) và \(\overrightarrow b \)bằng vecto \(\overrightarrow {AC} \).
Ta có viết: \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
LT – VD 1
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh \(\overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {AN} \)
Phương pháp giải:
Bước 1: Chứng minh \(\overrightarrow {PB} = \overrightarrow {NM} ;\;\overrightarrow {AN} = \overrightarrow {NC} \)
Bước 2: Tính tổng \(\overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {NM} + \overrightarrow {MC} = \overrightarrow {NC} = \overrightarrow {AN} \)
Lời giải chi tiết:
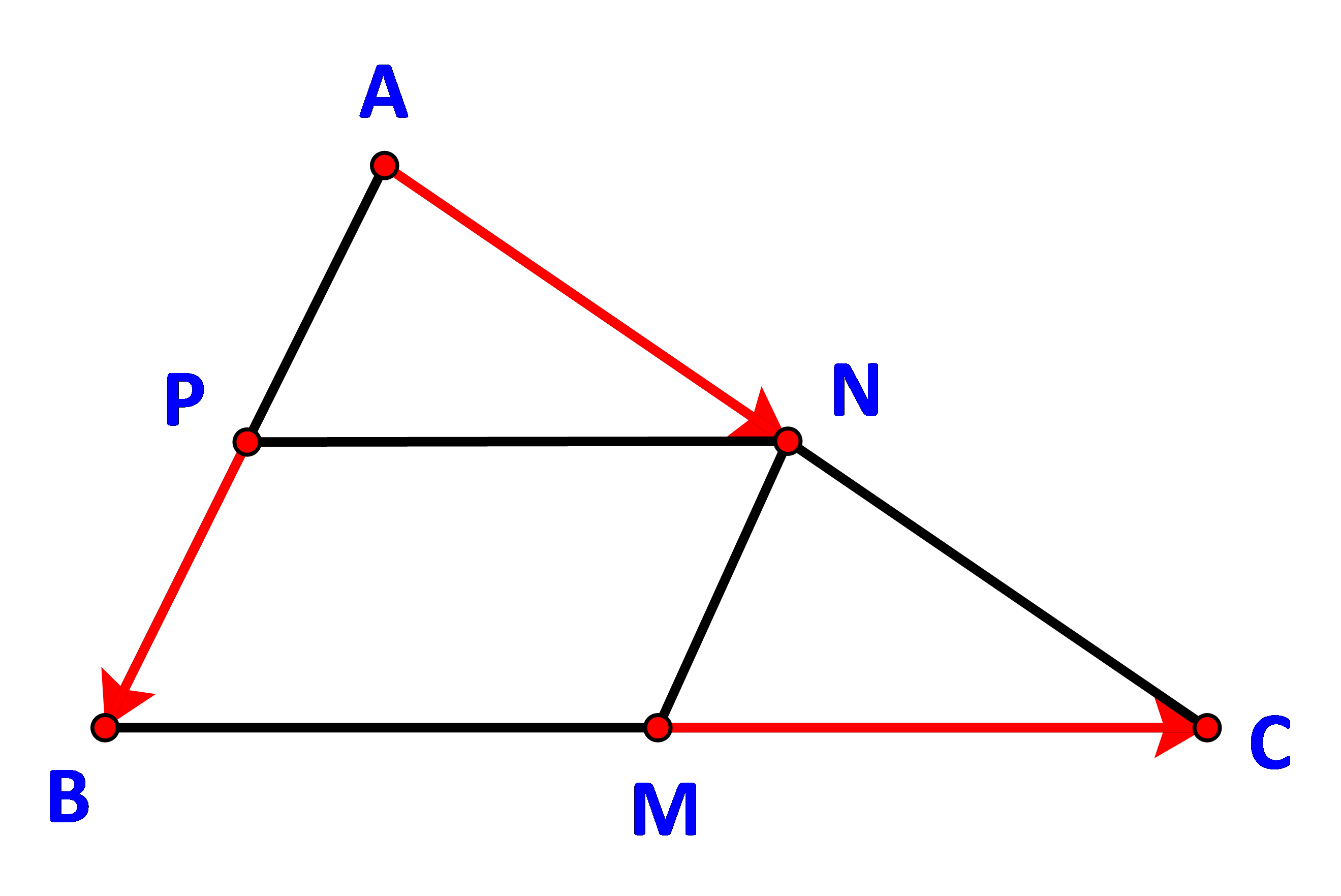
Do M, N, P lần lượt là trung điểm của BC, CA, AB
\( \Rightarrow MN = \frac{{AB}}{2} = PB\) và MN // PB.
\( \Rightarrow \overrightarrow {PB} = \overrightarrow {NM} \)
Ta có: \(\overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {NM} + \overrightarrow {MC} = \overrightarrow {NC} \)
Lại có: \(\overrightarrow {NC} = \overrightarrow {AN} \) (do N là trung điểm của AC)
Vậy \(\overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {AN} \)
Hoạt động 3
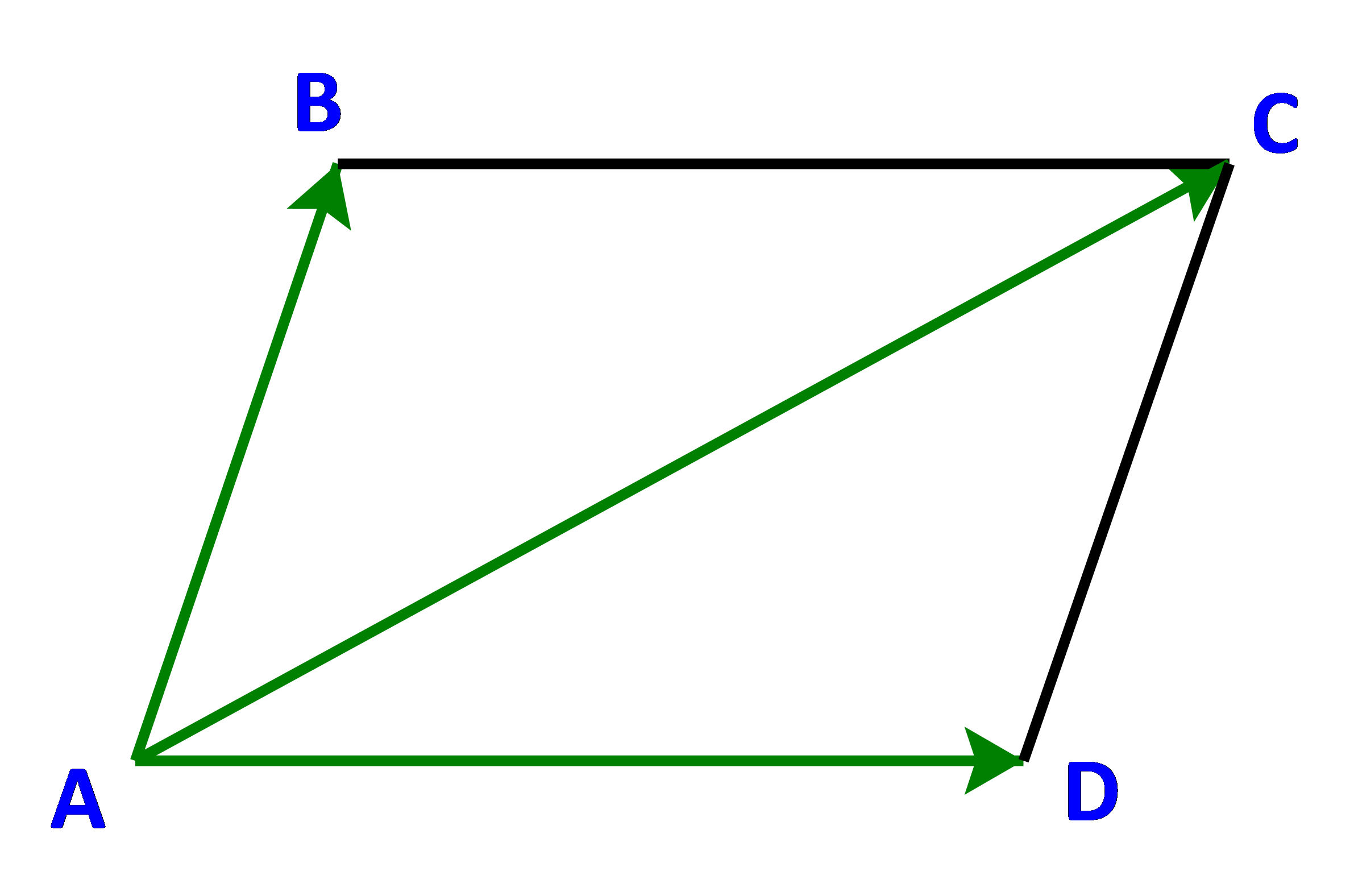
Cho ABCD là hình bình hành (Hình 52). So sánh:
a) Hai vecto \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \).
b) Vecto tổng \(\overrightarrow {AB} + \overrightarrow {AD} \) và vecto \(\overrightarrow {AC} \)
Phương pháp giải:
a) Nhận xét về giá, hướng và độ dài của hai vecto đó.
b) Thay vecto \(\overrightarrow {AD} \) bởi vecto \(\overrightarrow {BC} \)trong tổng rồi tính.
Lời giải chi tiết:
a) Ta có: \(\left\{ \begin{array}{l}AD//BC\\AD = BC\end{array} \right.\) (do tứ giác ABCD là hình bình hành)
\( \Rightarrow \overrightarrow {AD} = \overrightarrow {BC} \)
b) Ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
LT-VD 2
Hãy giải thích hướng đi của thuyền ở Hình 48.

Phương pháp giải:
Bước 1: Gọi tên các lực tác động lên thuyền.
Bước 2: Vận dụng quy tắc hình bình hành tính tổng hai lực.
Lời giải chi tiết:
Gọi vecto \(\overrightarrow {AB} ,\overrightarrow {AD} \) là các vecto biểu diễn lực mà hai người cùng tác động lên điểm A của thuyền.
Khi đó thuyền chịu một lực là tổng hai lực kéo đó.
Vậy thuyền đi theo hướng của vecto tổng \(\overrightarrow {AB} + \overrightarrow {AD} \)
Vẽ hình bình hành ABCD. Khi đo ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Vậy khi hai người cùng kéo, thuyền đi theo vecto đường chéo của hình bình hành tạo bởi hai lực kéo của hai người.
LT-VD 3
Cho hình bình hành ABCD và điểm E bất kì. Chứng minh: \(\overrightarrow {AB} + \overrightarrow {CE} + \overrightarrow {AD} = \overrightarrow {AE} \).
Phương pháp giải:
Bước 1: Sử dụng tính chất giao hoán, ta tính: \((\overrightarrow {AB} + \overrightarrow {AD} ) + \overrightarrow {CE} \)
Bước 2: Vận dụng quy tắc hình bình hành, chỉ ra \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)từ đó suy ra đpcm.
Lời giải chi tiết:
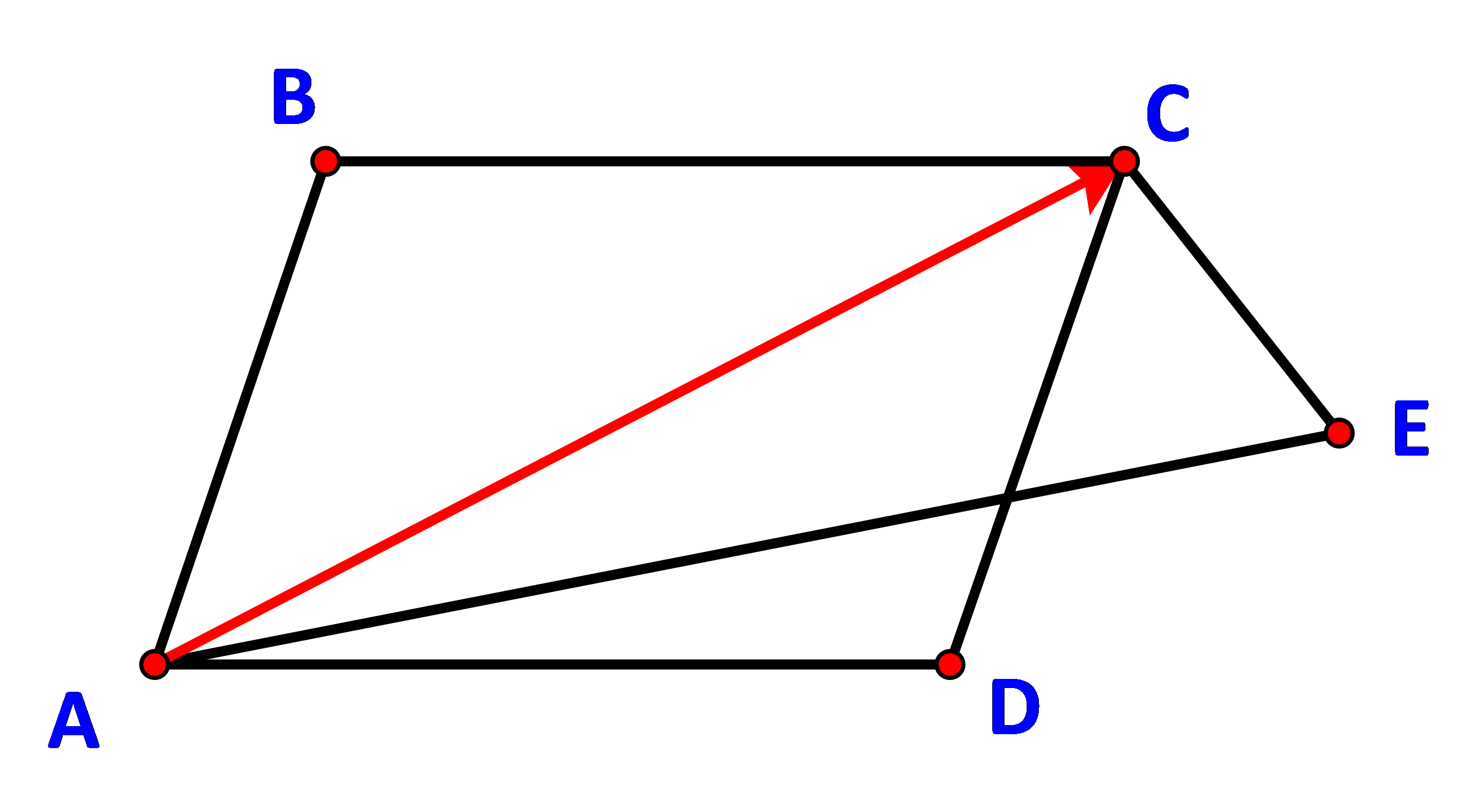
Ta có: \(\overrightarrow {AB} + \overrightarrow {CE} + \overrightarrow {AD} = (\overrightarrow {AB} + \overrightarrow {AD} ) + \overrightarrow {CE} \) (tính chất giao hoán)
Mà theo quy tắc hình bình hành ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Suy ra \(\overrightarrow {AB} + \overrightarrow {CE} + \overrightarrow {AD} = \overrightarrow {AC} + \overrightarrow {CE} = \overrightarrow {AE} \)
Vậy \(\overrightarrow {AB} + \overrightarrow {CE} + \overrightarrow {AD} = \overrightarrow {AE} \) với điểm E bất kì.

