Hoạt động 3
Trên nửa đường tròn đơn vị ta có dây cung MN song song với trục Ox và \(\widehat {xOM} = \alpha \).
a) Chứng minh \(\widehat {xON} = {180^o} - \alpha \)
b) Biểu diễn giá trị lượng giác của góc \({180^o} - \alpha \) theo giá trị lượng giác của góc \(\alpha \).
Phương pháp giải:
a) Quan sát hình 6, dựa vào các góc đồng vị và tam giác cân để suy ra \(\widehat {xON} = {180^o} - \alpha \)
b) Trên hình vẽ, xác định các GTLG của \(\widehat {xON}\),so sánh với GTLG của góc \(\alpha \).
Lời giải chi tiết:
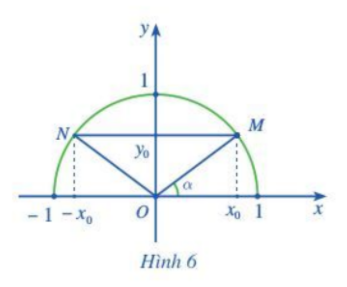
a) Do MN song song với Ox nên \(\alpha = \widehat {OMN} = \widehat {ONM} = \widehat {NOx'}\)
Mà \(\widehat {xON} = {180^o} - \widehat {NOx'} = {180^o} - \alpha \)
\( \Rightarrow \widehat {xON} = {180^o} - \alpha \)
b) Dễ thấy: Điểm N đối xứng với M qua trục Oy
\( \Rightarrow N( - {x_0};{y_0})\)
Lại có: điểm N biểu diễn góc \({180^o} - \alpha \)
\( \Rightarrow \left\{ \begin{array}{l}\sin ({180^o} - \alpha ) = {y_N} = {y_0}\\\cos ({180^o} - \alpha ) = {x_N} = - {x_0}\end{array} \right.\);
Mà: \(\sin \alpha = {y_0};\;\cos \alpha = {x_0}\)
\( \Rightarrow \left\{ \begin{array}{l}\sin ({180^o} - \alpha ) = \sin \alpha \;\\\cos ({180^o} - \alpha ) = - \cos \alpha \end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}\tan ({180^o} - \alpha ) = - \tan \alpha \;\\\cot ({180^o} - \alpha ) = - \cot \alpha \end{array} \right.\)
Luyện tập – vận dụng 1
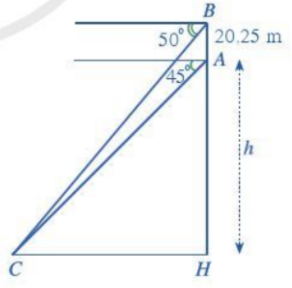
Hãy tính chiều cao h của đỉnh Lũng Cú so với chân núi trong bài toán ở phần mở đầu.
Phương pháp giải:
Bước 1: Tính \(\widehat {ACH},\widehat {BCH}\)
Bước 2: Tính \(\tan \widehat {ACH},\tan \widehat {BCH}\) theo h.
Bước 3: Giải phương trình ẩn h và kết luận.
Lời giải chi tiết:
\(\left\{ \begin{array}{l}\widehat {ACH} = {45^o}\\\widehat {BCH} = {50^o}\end{array} \right.\) (hai góc đồng vị)
Mà \(\tan \widehat {ACH} = \frac{{AH}}{{CH}} \Rightarrow \tan {45^o} = \frac{h}{{CH}} \Leftrightarrow CH = h\)
Lại có: \(\tan \widehat {BCH} = \frac{{BH}}{{CH}} \Rightarrow \tan {50^o} = \frac{{h + 20,25}}{h}\)
\(\begin{array}{l} \Leftrightarrow h.\tan {50^o} = h + 20,25\\ \Leftrightarrow h = \frac{{20,25}}{{\tan {{50}^o} - 1}} \approx 105,6\end{array}\)
Vậy chiều cao của đỉnh Lũng cú so với chân núi là khoảng 105,6m.

