Đề bài
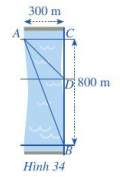
Một người đứng ở điểm A trên một bờ sông rộng 300 m, chèo thuyền đến vị trí D, sau đó chạy bộ đến vị trí B cách C một khoảng 800 m như Hình 34. Vận tốc chèo thuyền là 6 km/h, vận tốc chạy bộ là 10 km/h và giả sử vận tốc dòng nước không đáng kể. Tính khoảng cách từ vị trí C đến D, biết tổng thời gian người đó chèo thuyền và chạy bộ từ A đến B là 7,2 phút.
Phương pháp giải - Xem chi tiết
- Gọi khoảng cách từ C đến D là x m (x>0)
- Biểu diễn DB, AD theo x.
- Biểu diễn đi từ A đến D và đi từ D đến B theo x.
- Lập phương trình và giải.
Lời giải chi tiết
Đổi 300 m =0,3 km, 800 m = 0,8 km
7,2 phút =0,12(h)
Gọi khoảng cách từ C đến D là x (km) (0,8>x>0)
Khi đó, DB=0,8-x (km)
Theo định lý Py-ta-go ta có: \(AD = \sqrt {A{C^2} + C{D^2}} \)\( = \sqrt {0,{3^2} + {{\left( {0,8 - x} \right)}^2}} \) (km)
Thời gian đi từ A đến D là: \(\frac{{\sqrt {0,{3^2} + {{\left( {0,8 - x} \right)}^2}} }}{6}\left( h \right)\)
Thời gian đi từ D đến B là: \(\frac{{0,8 - x}}{{10}}\left( h \right)\)
Tổng thời gian người đó chèo thuyền và chạy bộ từ A đến B là 7,2 phút nên ta có phương trình:
\(\begin{array}{l}\frac{{\sqrt {0,{3^2} + {{\left( {0,8 - x} \right)}^2}} }}{6} + \frac{{0,8 - x}}{{10}} = 0,12\\ \Leftrightarrow \sqrt {0,{3^2} + {{\left( {0,8 - x} \right)}^2}} .5 + 3.\left( {0,8 - x} \right) = 0,12.30\\ \Leftrightarrow 5.\sqrt {0,{3^2} + {{\left( {0,8 - x} \right)}^2}} - 3x - 1,2 = 0\\ \Leftrightarrow 5.\sqrt {0,{3^2} + {{\left( {0,8 - x} \right)}^2}} = 3x + 1,2\\ \Leftrightarrow 25.\left[ {0,{3^2} + {{\left( {0,8 - x} \right)}^2}} \right] = {\left( {3x + 1,2} \right)^2}\\ \Leftrightarrow 25.\left( {{x^2} - 1,6x + 0,73} \right) = 9{x^2} + 7,2x + 1,44\\ \Leftrightarrow 16{x^2} - 47,2x + 16,81 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{{59 + 30\sqrt 2 }}{{40}} > 0,8\left( {ktm} \right)\\x = \frac{{59 - 30\sqrt 2 }}{{40}} \approx 0,414\left( {tm} \right)\end{array} \right.\end{array}\)
Ta bình phương được do \(x > 0 \Rightarrow 3x + 1,2 > 0\)
Vậy khoảng cách từ vị trí C đến D là 414m.

