Đề bài
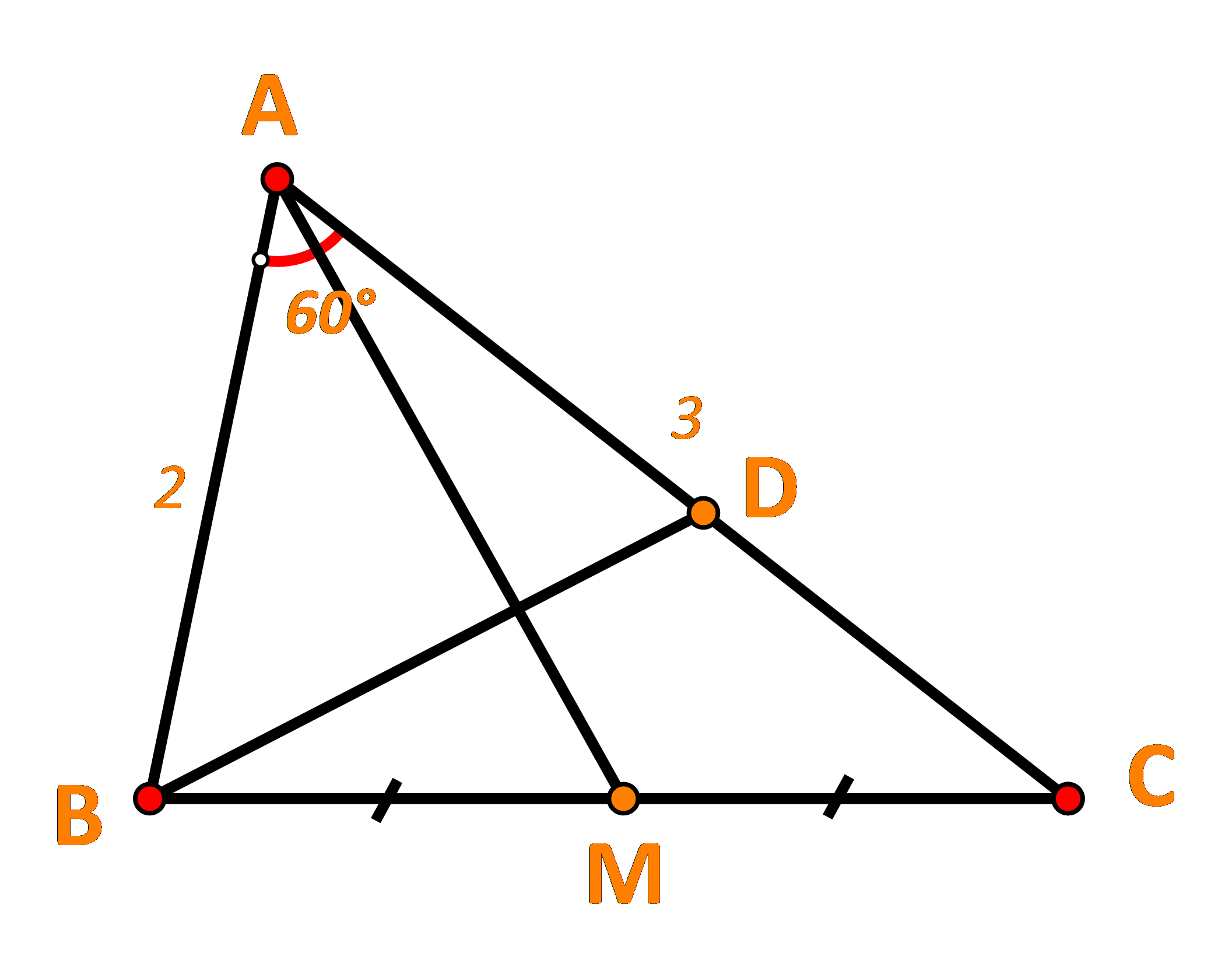
Cho tam giác ABC có AB=2,AC=3,^BAC=60o. Gọi M là trung điểm của đoạn thẳng BC. Điểm D thỏa mãn →AD=712→AC.
a) Tính →AB.→AC
b) Biểu diễn →AM,→BD theo →AB,→AC
c) Chứng minh AM⊥BD.
Phương pháp giải - Xem chi tiết
+) Tính →AB.→AC bằng công thức →AB.→AC=|→AB|.|→AC|.cos(→AB,→AC)=AB.AC.cos^BAC
+) M là trung điểm BC ⇔→AB+→AC=2→AM với điểm A bất kì.
+) AM⊥BD⇔→AM.→BD=0
Lời giải chi tiết
a) →AB.→AC=2.3.cos^BAC=6.cos60o=3
b)
Ta có: →AB+→AC=2→AM(do M là trung điểm của BC)
⇔→AM=12→AB+12→AC
+) →BD=→AD−→AB=712→AC−→AB
c) Ta có:
→AM.→BD=(12→AB+12→AC)(712→AC−→AB)=724→AB.→AC−12→AB2+724→AC2−12→AC.→AB=−12AB2+724AC2−524→AB.→AC=−12.22+724.32−524.3=0
⇒AM⊥BD

