Đường kính và dây của đường tròn

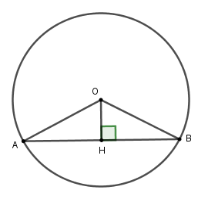
Kẻ $OH \bot AB$ tại $H$ suy ra $H$ là trung điểm của $AB$.

Xét tam giác $OHB$ vuông tại $H$ có $OH = 3;OB = 5$. Theo định lý Pytago ta có $HB = \sqrt {O{B^2} - O{H^2}}  = \sqrt {{5^2} - {3^2}}  = 4$

Mà $H$ là trung điểm của $AB$ nên $AB = 2HB = 8\,cm$

Vậy $AB = 8\,cm$.

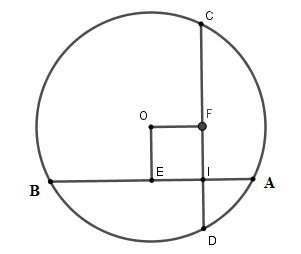
Xét đường tròn tâm $\left( O \right)$,

Kẻ $OE \bot AB$ tại $E$ suy ra $E$ là trung điểm của $AB$, kẻ $OF \bot CD$ tại $F$.

Vì dây $AB = CD$ nên $OE = OF$ (hai dây bằng nhau cách đều tâm)

Xét tứ giác $OEIF$ có $\widehat E = \widehat F = \widehat I = 90^\circ $ nên $OEIF$ là hình chữ nhật và $OE = OF$ nên $OEIF$ là hình vuông$ \Rightarrow OE = OF = EI$

Mà $AB = IA + IB = 6\,cm \Rightarrow EB = 3\,cm \Rightarrow EI = IB - EB = 1\,cm$ nên $OE = OF = 1\,cm$

Vậy tổng khoảng cách từ tâm đến hai dây $AB,CD$ là $2\,cm$.

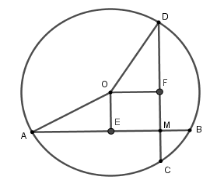
Xét đường tròn tâm $\left( O \right)$,

Kẻ $OE \bot AB$ tại $E$ suy ra $E$ là trung điểm của $AB$, kẻ $OF \bot CD$ tại $F$ suy ra $F$ là trung điểm của $CD$,

Xét tứ giác $OEMF$ có $\widehat E = \widehat F = \widehat M = 90^\circ $ nên $OEIF$ là hình chữ nhật, suy ra $FM = OE$.

Ta có $CD = 12\,cm \Rightarrow FC = 6\,cm$ mà $MC = 2\,cm \Rightarrow FM = FC - MC = 4\,cm$ nên $OE = \,4cm$

Vậy khoảng cách từ tâm $O$ đến dây $AB$ là $4\,cm$

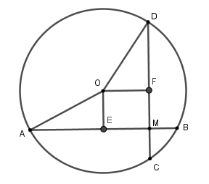
Lấy $E$; $F$ lần lượt là trung điểm của hai dây $AB$ và $CD$. Khi đó 

\(OE \bot AB;\,OF \bot AC\) lại có \(\widehat {FME} = 90^\circ \) nên \(OEMF\) là hình chữ nhật. Suy ra $OE=MF=CF-MC=4 \,\ cm.$

Xét đường tròn tâm $\left( O \right)$,

Có $OE = \,4\,cm$, $E$ là trung điểm của $AB$ nên $AE = \dfrac{{14}}{2} = 7cm$

Áp dụng định lý Pytago cho tam giác vuông $OEA$ ta có $OA = \sqrt {A{E^2} + O{E^2}}  = \sqrt {65} $ nên $R = \sqrt {65} $

Lại có $OD = \sqrt {65} \,\ cm ;FD = 6 \,\ cm$ nên áp dụng định lý Pytago cho tam giác vuông $OFD$ ta có

$OF = \sqrt {O{D^2} - F{D^2}}  = \sqrt {29} \,\ cm$. Do đó khoảng cách từ tâm đến dây $CD$ là $\sqrt {29} $$cm$ .

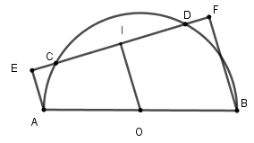
Lấy $I$ là trung điểm của $EF$

Xét tứ giác $AEFB$ có $AE\,{\rm{//}}FB$ (vì cùng vuông với $EF$) nên $AEFB$ là hình thang vuông tại $E;F$.

Ta có $OI$ là đường trung bình của hình thang $AEFB$ nên $OI\,{\rm{//}}\,AE{\rm{//}}FB$$ \Rightarrow OI \bot EF$

Hay $OI \bot CD$ nên $I$ là trung điểm của $CD$ ( quan hệ giữa dây và đường kính)

Ta có $IE = IF;IC = ID \Rightarrow IE - IC = IF - ID \Leftrightarrow EC = DF$.

Kẻ đường thẳng qua $O$ vuông góc với $AC$ tại $E$ và cắt $BD$ tại $F$ thì $EF \bot BD$ tại $F$ vì $AC{\rm{//}}BD.$

Xét hai tam giác vuông $OEA$ và tam giác $OFB$ có $OB = OA;\widehat {EAO} = \widehat {FBO}$ (so le trong)

Nên $\Delta AEO = \Delta BFO$ (ch-gn) $ \Rightarrow OE = OF$$ \Rightarrow AC = DB$ (hai dây cách đều tâm thì bằng nhau).

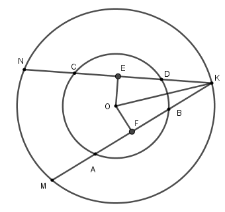
Xét đường tròn $\left( {O;OB} \right)$

Kẻ $OE \bot CD;OF \bot AB$ tại $E,F$ mà $CD < AB \Rightarrow OE > OF$ ( dây nào lớn hơn thì gần tâm hơn)

Xét đường tròn $\left( {O;OK} \right)$ có $OE \bot KN;OF \bot KM$ tại $E,F$ mà $OE > OF \Rightarrow KN < KM$( liên hệ giữa dây và khoảng cách từ tâm đến dây)

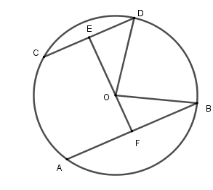
Kẻ đường thẳng qua $O$ vuông góc với $CD$ tại $E$ và cắt $AB$ tại $F$ thì $EF \bot AB$ vì $AB\,{\rm{//}}\,CD$.

Khi đó $E$ là trung điểm của $CD$ và $F$ là trung điểm của $AB$ ( đường kính vuông góc với dây thì đi qua trung điểm dây đó). Nên $ED = 6\,cm;\,FB = 8\,cm$; $OD = OB = 10\,cm$

Áp dụng định lý Pytago cho tam giác vuông $OED$ ta được $OE = \sqrt {O{D^2} - E{D^2}}  = 8\,cm$

Áp dụng định lý Pytago cho tam giác vuông $OFB$ ta được $OF = \sqrt {O{B^2} - F{B^2}}  = 6\,cm$

 Vậy khoảng cách giữa hai dây là $EF = OE + OF = 14\,cm$.

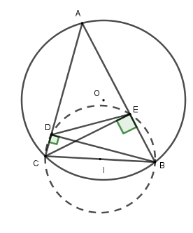
Lấy $I$ là trung điểm của $BC$

Xét tam giác vuông $BDC$ có $DI$ là đường trung tuyến ứng với cạnh huyền nên $DI = IB = IC = \dfrac{{BC}}{2}$

Xét tam giác vuông $BEC$ có $EI$ là đường trung tuyến ứng với cạnh huyền nên $EI = IB = IC = \dfrac{{BC}}{2}$

Từ đó $ID = IE = IB = IC = \dfrac{{BC}}{2}$ hay bốn điểm $B,C,D,E$ cùng thuộc đường tròn $\left( {I;\dfrac{{BC}}{2}} \right)$

Xét $\left( {I;\dfrac{{BC}}{2}} \right)$ có $BC$ là đường kính  và $DE$ là dây không đi qua tâm nên $BC > DE$.

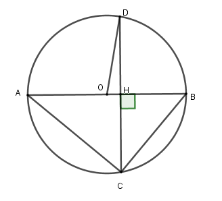
Xét $\left( O \right)$ có $AB \bot CD$ tại $H$ và $AB$ là đường kính nên $H$ là trung điểm của $CD$$ \Rightarrow HD = HC = \dfrac{{CD}}{2} = 6\,cm$

Vì $AB = 14 \Rightarrow OA = OB = OD = \dfrac{{14}}{2} = 7\,cm$.

Áp dụng định lý Pytago cho tam giác vuông $OHD$ ta được $OH = \sqrt {O{D^2} - D{H^2}}  = \sqrt {13} $

Khi đó $HA = OA + OH = 7 + \sqrt {13} \,cm$.

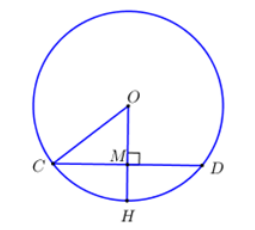
Do \(OM \bot CD \Rightarrow M\) là trung điểm của \(CD \Rightarrow CM = \dfrac{1}{2}CD = \dfrac{1}{2}.16 = 8\,\,\left( {cm} \right).\)

Gọi \(R\) là bán kính của đường tròn \( \Rightarrow OC = R\).

Ta có \(OM = OH - HM = R - 4\).

Áp dụng định lí Pytago trong tam giác vuông \(OMC\) ta có:

\(\begin{array}{l}O{C^2} = C{M^2} + O{M^2} \Rightarrow {R^2} = {8^2} + {\left( {R - 4} \right)^2}\\ \Leftrightarrow {R^2} = 64 + {R^2} - 8R + 16 \Leftrightarrow R = 10\,\,\left( {cm} \right)\end{array}\)