Câu hỏi:
2 năm trước
Cho đường tròn $\left( {O;R} \right)$có hai dây $AB,CD$ bằng nhau và vuông góc với nhau tại $I$. Giả sử $IA = 2cm;IB = 4cm$ . Tổng khoảng cách từ tâm $O$ dây $AB,CD$ là
Trả lời bởi giáo viên
Đáp án đúng: d
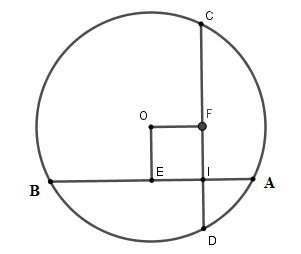
Xét đường tròn tâm $\left( O \right)$,
Kẻ $OE \bot AB$ tại $E$ suy ra $E$ là trung điểm của $AB$, kẻ $OF \bot CD$ tại $F$.
Vì dây $AB = CD$ nên $OE = OF$ (hai dây bằng nhau cách đều tâm)
Xét tứ giác $OEIF$ có $\widehat E = \widehat F = \widehat I = 90^\circ $ nên $OEIF$ là hình chữ nhật và $OE = OF$ nên $OEIF$ là hình vuông$ \Rightarrow OE = OF = EI$
Mà $AB = IA + IB = 6\,cm \Rightarrow EB = 3\,cm \Rightarrow EI = IB - EB = 1\,cm$ nên $OE = OF = 1\,cm$
Vậy tổng khoảng cách từ tâm đến hai dây $AB,CD$ là $2\,cm$.
Hướng dẫn giải:
Sử dụng kiến thức “Hai dây bằng nhau thì cách đều tâm”
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
