Câu hỏi:
2 năm trước
Cho đường tròn \(\left( {O;R} \right)\) và một dây \(CD.\) Từ \(O\) kẻ tia vuông góc với \(CD\) tại \(M,\) cắt \(\left( {O;R} \right)\) tại \(H\) . Biết \(CD = 16cm;\,MH = 4cm.\) Bán kính \(R\) bằng
Trả lời bởi giáo viên
Đáp án đúng: d
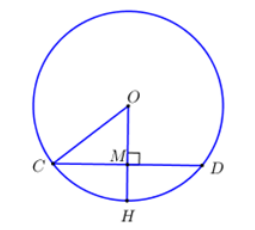
Do \(OM \bot CD \Rightarrow M\) là trung điểm của \(CD \Rightarrow CM = \dfrac{1}{2}CD = \dfrac{1}{2}.16 = 8\,\,\left( {cm} \right).\)
Gọi \(R\) là bán kính của đường tròn \( \Rightarrow OC = R\).
Ta có \(OM = OH - HM = R - 4\).
Áp dụng định lí Pytago trong tam giác vuông \(OMC\) ta có:
\(\begin{array}{l}O{C^2} = C{M^2} + O{M^2} \Rightarrow {R^2} = {8^2} + {\left( {R - 4} \right)^2}\\ \Leftrightarrow {R^2} = 64 + {R^2} - 8R + 16 \Leftrightarrow R = 10\,\,\left( {cm} \right)\end{array}\)
Hướng dẫn giải:
Sử dụng định lí Pytago trong tam giác vuông.
Câu hỏi khác
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
