Câu hỏi:
3 năm trước
Cho đường tròn $\left( {O;R} \right)$có hai dây $AB,CD$ vuông góc với nhau ở $M$. Biết$AB = 16\,cm;\,CD = 12\,cm;\,MC = 2\,cm$. Khoảng cách từ tâm $O$ đến dây $AB$ là
Trả lời bởi giáo viên
Đáp án đúng: a
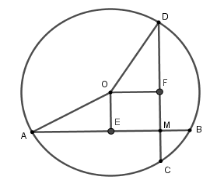
Xét đường tròn tâm $\left( O \right)$,
Kẻ $OE \bot AB$ tại $E$ suy ra $E$ là trung điểm của $AB$, kẻ $OF \bot CD$ tại $F$ suy ra $F$ là trung điểm của $CD$,
Xét tứ giác $OEMF$ có $\widehat E = \widehat F = \widehat M = 90^\circ $ nên $OEIF$ là hình chữ nhật, suy ra $FM = OE$.
Ta có $CD = 12\,cm \Rightarrow FC = 6\,cm$ mà $MC = 2\,cm \Rightarrow FM = FC - MC = 4\,cm$ nên $OE = \,4cm$
Vậy khoảng cách từ tâm $O$ đến dây $AB$ là $4\,cm$
Hướng dẫn giải:
Kẻ các đường vuông góc từ tâm đến dây. Sử dụng mối liên hệ giữa dây và đường kính và tính chất hình chữ nhật để suy ra khoảng cách.

