Câu hỏi:
3 năm trước
Cho đường tròn $\left( O \right)$ đường kính $AB = 14cm$, dây $CD$ có độ dài $12cm$ vuông góc với $AB$ tại $H$ nằm giữa $O$ và $B$. Độ dài $HA$ là
Trả lời bởi giáo viên
Đáp án đúng: a
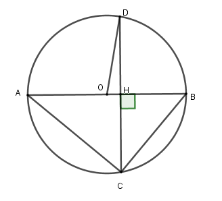
Xét $\left( O \right)$ có $AB \bot CD$ tại $H$ và $AB$ là đường kính nên $H$ là trung điểm của $CD$$ \Rightarrow HD = HC = \dfrac{{CD}}{2} = 6\,cm$
Vì $AB = 14 \Rightarrow OA = OB = OD = \dfrac{{14}}{2} = 7\,cm$.
Áp dụng định lý Pytago cho tam giác vuông $OHD$ ta được $OH = \sqrt {O{D^2} - D{H^2}} = \sqrt {13} $
Khi đó $HA = OA + OH = 7 + \sqrt {13} \,cm$.
Hướng dẫn giải:
+) Sử dụng mối liên hệ giữa dây và đường kính: “ Đường kính vuông góc với dây thì đi qua trung điểm của dây đó”
+) Sử dụng định lý Pytago

