Cho đường tròn $\left( {O;10\,cm} \right).$ Dây $AB$ và $CD$ song song, có độ dài lần lượt là $16cm$ và $12\,cm$ .Tính khoảng cách giữa hai dây.
Trả lời bởi giáo viên
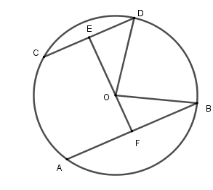
Kẻ đường thẳng qua $O$ vuông góc với $CD$ tại $E$ và cắt $AB$ tại $F$ thì $EF \bot AB$ vì $AB\,{\rm{//}}\,CD$.
Khi đó $E$ là trung điểm của $CD$ và $F$ là trung điểm của $AB$ ( đường kính vuông góc với dây thì đi qua trung điểm dây đó). Nên $ED = 6\,cm;\,FB = 8\,cm$; $OD = OB = 10\,cm$
Áp dụng định lý Pytago cho tam giác vuông $OED$ ta được $OE = \sqrt {O{D^2} - E{D^2}} = 8\,cm$
Áp dụng định lý Pytago cho tam giác vuông $OFB$ ta được $OF = \sqrt {O{B^2} - F{B^2}} = 6\,cm$
Vậy khoảng cách giữa hai dây là $EF = OE + OF = 14\,cm$.
Hướng dẫn giải:
Sử dụng liên hệ giữa dây và đường kính để áp dụng định lý Pytago cho tam giác vuông phù hợp.

