Trả lời bởi giáo viên
Đáp án đúng: c
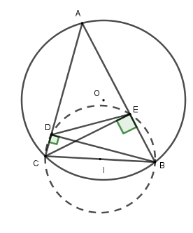
Lấy $I$ là trung điểm của $BC$
Xét tam giác vuông $BDC$ có $DI$ là đường trung tuyến ứng với cạnh huyền nên $DI = IB = IC = \dfrac{{BC}}{2}$
Xét tam giác vuông $BEC$ có $EI$ là đường trung tuyến ứng với cạnh huyền nên $EI = IB = IC = \dfrac{{BC}}{2}$
Từ đó $ID = IE = IB = IC = \dfrac{{BC}}{2}$ hay bốn điểm $B,C,D,E$ cùng thuộc đường tròn $\left( {I;\dfrac{{BC}}{2}} \right)$
Xét $\left( {I;\dfrac{{BC}}{2}} \right)$ có $BC$ là đường kính và $DE$ là dây không đi qua tâm nên $BC > DE$.
Hướng dẫn giải:
Bước 1: Tìm đường tròn đi qua bốn đỉnh $B,D,C,E$
Bước 2: Sử dụng liên hệ giữa dây và đường kính.
Câu hỏi khác
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
