Cho hình vẽ, trong đó \(DE{\rm{//}}BC\), \(AE = 12,\,DB = 18,\,AC = 36\). Độ dài \(AB\) bằng:
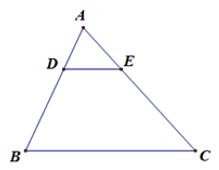
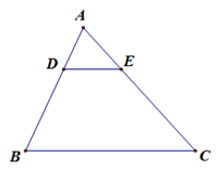
Vì \(DE{\rm{//}}BC\), theo định lý Ta-lét ta có \(\dfrac{{AD}}{{DB}} = \dfrac{{AE}}{{EC}}\) \( \Leftrightarrow \dfrac{{AD}}{{18}} = \dfrac{{12}}{{36 - 12}}\) \( \Leftrightarrow \dfrac{{AD}}{{18}} = \dfrac{{12}}{{24}}\) \( \Leftrightarrow AD = \dfrac{{18.12}}{{24}} = 9\)
\( \Rightarrow AB = AD + DB = 9 + 18 = 27\).
Chọn câu trả lời đúng:
Cho hình thang \(ABCD\) (\(AB{\rm{//}}CD\)), \(O\) là giao điểm của \(AC\) và \(BD\). Xét các khẳng định sau:
(I) \(\dfrac{{OA}}{{OC}} = \dfrac{{AB}}{{CD}}\) (II) \(\dfrac{{OB}}{{OC}} = \dfrac{{BC}}{{AD}}\) (III) \(OA.OD = OB.OC\)
Số khẳng định đúng trong các khẳng định trên là:
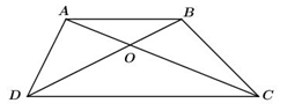
Vì \(AB\,{\rm{//}}\,CD\), áp dụng định lý Talet, ta có:
\(\dfrac{{OA}}{{OC}} = \dfrac{{AB}}{{CD}} = \dfrac{{OB}}{{OD}}\)\( \Rightarrow \dfrac{{OA}}{{OC}} = \dfrac{{OB}}{{OD}} \Leftrightarrow OA.OD = OB.OC\)
\( \Rightarrow \)Khẳng định (I) \(\dfrac{{OA}}{{OC}} = \dfrac{{AB}}{{CD}}\) đúng, khẳng định (II) \(\dfrac{{OB}}{{OC}} = \dfrac{{BC}}{{AD}}\) sai, khẳng định (III) \(OA.OD = OB.OC\) đúng.
Vậy có \(2\) khẳng định đúng.
Cho biết \(M\) thuộc đoạn thẳng \(AB\) thỏa mãn \(\dfrac{{AM}}{{MB}} = \dfrac{3}{8}\). Đặt \(\dfrac{{AM}}{{AB}} = k\), số \(k\) thỏa mãn điều kiện nào dưới đây?
Ta có:
\(\dfrac{{AM}}{{MB}} = \dfrac{3}{8}\)\( \Rightarrow \dfrac{{AM}}{{MB + AM}} = \dfrac{3}{{8 + 3}}\) \( \Rightarrow \dfrac{{AM}}{{AB}} = \dfrac{3}{{11}}\) hay \(k = \dfrac{3}{{11}}\) nên B sai, C đúng.
Dễ thấy \(\dfrac{3}{{11}} < \dfrac{3}{8}\) nên A sai; \(\dfrac{3}{{11}} < \dfrac{1}{2}\) nên D sai.
Tam giác \(MEF\) là tam giác gì? Chọn đáp án đúng nhất.
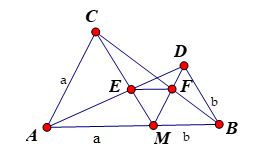
Từ câu trước ta có \(ME = MF \Rightarrow \Delta EMF \) cân tại \(M\) .
Ta có \(\widehat {AMC} + \widehat {EMF} + \widehat {DMB} = 180^\circ \) mà \(\widehat {AMC} = \widehat {DMB} = 60^\circ \) (tính chất tam giác đều), nên
\(\begin{array}{l}\widehat {EMF} = 180^\circ - \widehat {CMA} - \widehat {DMB}\\ = 180^\circ - 60^\circ - 60^\circ = 60^\circ \end{array}\)
Từ đó \(MEF\) là tam giác cân có một góc bằng \(60^\circ \) nên nó là tam giác đều.
Đặt \(MA = a,MB = b\). Tính \(ME,MF\) theo \(a\) và \(b\).
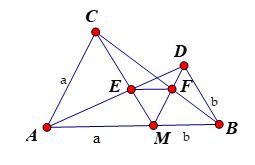
Vì các tam giác \(AMC\) và \(BMD\) đều nên \(\widehat {BMD} = \widehat {MAC} = 60^\circ \Rightarrow MD{\rm{//}}AC\) (vì hai góc ở vị trí đồng vị)
Vì \(MD{\rm{//}}AC\) nên theo hệ quả định lý Talet cho hai tam giác \(DEM\) và \(AEC\) ta có \(\dfrac{{ME}}{{EC}} = \dfrac{{MD}}{{AC}} = \dfrac{b}{a}\)
Suy ra
\(\begin{array}{l}\dfrac{{ME}}{{EC}} = \dfrac{b}{a} \Rightarrow \dfrac{{ME}}{{ME + EC}} = \dfrac{b}{{b + a}}\\ \Rightarrow \dfrac{{ME}}{a} = \dfrac{b}{{b + a}} \Rightarrow ME = \dfrac{{ab}}{{b + a}}\end{array}\)
Tương tự \(MF = \dfrac{{ba}}{{a + b}}\) .
Vậy \(ME = MF = \dfrac{{ab}}{{b + a}}\).
Đặt \(MA = a,MB = b\). Tính \(ME,MF\) theo \(a\) và \(b\).

Vì các tam giác \(AMC\) và \(BMD\) đều nên \(\widehat {BMD} = \widehat {MAC} = 60^\circ \Rightarrow MD{\rm{//}}AC\) (vì hai góc ở vị trí đồng vị)
Vì \(MD{\rm{//}}AC\) nên theo hệ quả định lý Talet cho hai tam giác \(DEM\) và \(AEC\) ta có \(\dfrac{{ME}}{{EC}} = \dfrac{{MD}}{{AC}} = \dfrac{b}{a}\)
Suy ra
\(\begin{array}{l}\dfrac{{ME}}{{EC}} = \dfrac{b}{a} \Rightarrow \dfrac{{ME}}{{ME + EC}} = \dfrac{b}{{b + a}}\\ \Rightarrow \dfrac{{ME}}{a} = \dfrac{b}{{b + a}} \Rightarrow ME = \dfrac{{ab}}{{b + a}}\end{array}\)
Tương tự \(MF = \dfrac{{ba}}{{a + b}}\) .
Vậy \(ME = MF = \dfrac{{ab}}{{b + a}}\).
Cho hình vẽ, trong đó \(AB{\rm{//}}CD\) và \(DE = EC\). Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
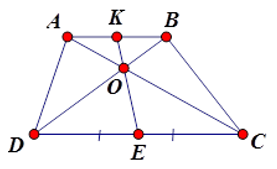
(I) \(\dfrac{{AK}}{{EC}} = \dfrac{{KB}}{{DE}}\) (II) \(\dfrac{{AK}}{{AB}} = \dfrac{{DE}}{{DC}}\)
(III) \(\dfrac{{AO}}{{OC}} = \dfrac{{AB}}{{DC}}\) (IV) \(\dfrac{{OK}}{{OE}} = \dfrac{{AB}}{{CD}}\)
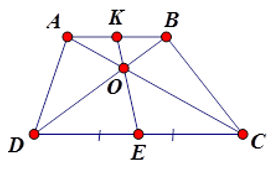
Theo định lý Ta-lét:
Vì \(AK{\rm{//}}EC\) nên \(\dfrac{{AK}}{{EC}} = \dfrac{{OK}}{{OE}} = \dfrac{{OA}}{{OC}}\) và \(BK{\rm{//}}ED\) nên \(\dfrac{{KB}}{{DE}} = \dfrac{{OK}}{{OE}} = \dfrac{{OB}}{{OD}}\) từ đó \(\dfrac{{AK}}{{EC}} = \dfrac{{KB}}{{DE}}\) nên (I) đúng.
Lại có \(\dfrac{{AK}}{{AB}} = \dfrac{1}{2};\dfrac{{DE}}{{DC}} = \dfrac{1}{2}\) nên \(\dfrac{{AK}}{{AB}} = \dfrac{{DE}}{{DC}}\) hay (II) đúng.
Do \(AB//CD \Rightarrow \dfrac{{OA}}{{OC}} = \dfrac{{OB}}{{OD}} = \dfrac{{AB}}{{CD}}\) hay (III) đúng.
Mà \(\dfrac{{OK}}{{OE}} = \dfrac{{AK}}{{EC}}\) và \(\dfrac{{AK}}{{EC}} = \dfrac{{\dfrac{1}{2}AB}}{{\dfrac{1}{2}DC}} = \dfrac{{AB}}{{CD}}\) nên \(\dfrac{{OK}}{{OE}} = \dfrac{{AB}}{{CD}}\) hay (IV) đúng.
Vậy cả \(4\) khẳng định đã cho đều đúng.
Chọn câu trả lời đúng: Cho hình bên, biết \(ED \bot AB,AC \bot AB\), tìm \(x\):
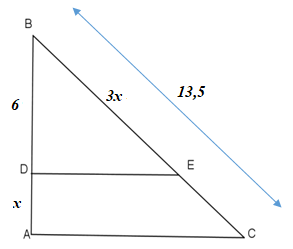
Ta có: \(ED \bot AB,AC \bot AB\)\( \Rightarrow DE{\rm{//}}AC\) (từ vuông góc đến song song), áp dụng định lý Talet, ta có:
\(\dfrac{{BD}}{{DA}} = \dfrac{{BE}}{{EC}}\) \( \Rightarrow \dfrac{6}{x} = \dfrac{{3x}}{{13,5 - 3x}}\) \( \Leftrightarrow 6\left( {13,5 - 3x} \right) = x.3x\) \( \Leftrightarrow 81 - 18x = 3{x^2}\) \( \Leftrightarrow 3{x^2} + 18x - 81 = 0\)
\( \Leftrightarrow {x^2} + 6x - 27 = 0\) \( \Leftrightarrow {x^2} + 9x - 3x - 27 = 0\) \( \Leftrightarrow x\left( {x + 9} \right) - 3\left( {x + 9} \right) = 0\) \( \Leftrightarrow \left( {x + 9} \right)\left( {x - 3} \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x + 9 = 0\\x - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 9\left( {loai} \right)\\x = 3\left( {TM} \right)\end{array} \right.\)
Vậy \(x = 3\).
Cho tam giác \(ABC\). Một đường thẳng song song song với \(BC\) cắt các cạnh \(AB\) và \(AC\) theo thứ tự tại \(D\) và \(E\). Qua \(E\) kẻ đường thẳng song song với \(CD\), cắt \(AB\) ở \(F\). Biết \(AB = 16, AF = 9\), độ dài \(AD\) là:
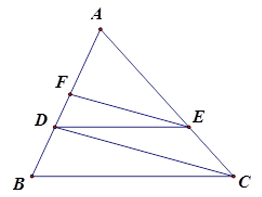
Áp dụng định lí Ta-lét :
Với \({\rm{EF//}}CD\) ta có: \(\dfrac{{AF}}{{AD}} = \dfrac{{AE}}{{AC}}\).
Với \(DE{\rm{//}}BC\) ta có: \(\dfrac{{AE}}{{AC}} = \dfrac{{AD}}{{AB}}\).
Suy ra \(\dfrac{{AF}}{{AD}} = \dfrac{{AD}}{{AB}}\), tức là \(AF.AB = A{D^2}\).
Vậy \(9.16 = A{D^2}\)\( \Leftrightarrow A{D^2} = 144 \Leftrightarrow AD = 12\) (cm).
Cho hình vẽ:
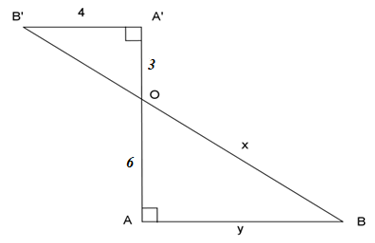
Giá trị biểu thức \(x - y\) là:
Áp dụng định lý Py-ta-go cho tam giác vuông \(OA'B'\), ta có:
\(\begin{array}{l}OA{'^2} + A'B{'^2} = OB{'^2}\\ \Leftrightarrow {3^2} + {4^2} = OB{'^2}\\ \Leftrightarrow OB{'^2} = 25\\ \Rightarrow OB' = 5\end{array}\)
\(A'B' \bot AA',\;AB \bot AA' \Rightarrow A'B'\parallel AB\) (Theo định lý từ vuông góc đến song song)
Áp dụng định lý Ta-let, ta có:
\(\dfrac{{OA'}}{{OA}} = \dfrac{{OB'}}{{OB}} = \dfrac{{A'B'}}{{AB}}\)
\( \Rightarrow \dfrac{3}{6} = \dfrac{5}{x} = \dfrac{4}{y}\)\( \Rightarrow \left\{ \begin{array}{l}x = \dfrac{{5.6}}{3} = 10\\y = \dfrac{{6.4}}{3} = 8\end{array} \right.\) hay \(x - y = 10 - 8 = 2\).
Tìm giá trị của \(x\) trên hình vẽ.
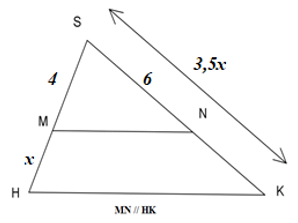
Vì \(MN{\rm{//}}HK\), áp dụng định lý Ta-let ta có:
\(\dfrac{{SM}}{{MH}} = \dfrac{{SN}}{{NK}}\) \( \Leftrightarrow \dfrac{4}{x} = \dfrac{6}{{3,5x - 6}}\) \( \Leftrightarrow 4\left( {3,5x - 6} \right) = 6x\) \( \Leftrightarrow 14x - 24 = 6x\) \( \Leftrightarrow 8x = 24 \Leftrightarrow x = 3\).
Vậy \(x = 3\).
Cho hình thang \(ABCD\) \(\left( {AB{\rm{//}}CD} \right)\) có \(BC = 15\,cm,AD = 12\,cm\). Điểm \(E\) thuộc cạnh \(AD\) sao cho \(AE = 4\). Qua \(E\) kẻ đường thẳng song song với \(CD\), cắt \(BC\) ở \(F\). Tính độ dài \(BF\).
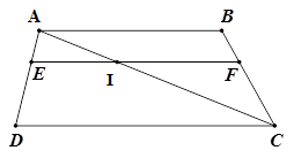
Gọi \(I\) là giao điểm của \(AC\) và \(EF\).
Xét tam giác \(ACB\) có \(IF{\rm{//}}AB\) nên theo định lý Ta-lét ta có:
\(\dfrac{{BF}}{{BC}} = \dfrac{{AI}}{{AC}} = \dfrac{{AE}}{{AD}} = \dfrac{4}{{12}} = \dfrac{1}{3}\) nên \(BF = \dfrac{1}{3}BC = \dfrac{1}{3}.15 = 5\left( {cm} \right)\).
Cho hình thang \(ABCD\) \(\left( {AB//CD} \right)\). Một đường thẳng song song với \(AB\) cắt các cạnh bên \(AD,BC\) theo thứ tự ở \(E,F\). Đẳng thức nào sau đây đúng?
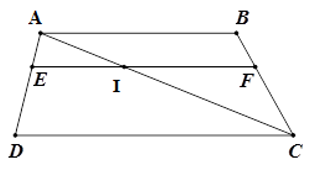
Gọi \(I\) là giao điểm của \(AC\) với \(EF\). Xét \(\Delta ADC\) có \(EI//DC\), theo định lý Ta-let ta có:
\(\dfrac{{AE}}{{AD}} = \dfrac{{AI}}{{AC}}\) (1)
Xét \(\Delta ABC\) có \(IF//AB\), theo định lý Ta-let ta có:
\(\dfrac{{AI}}{{AC}} = \dfrac{{BF}}{{BC}}\) (2)
Từ (1) và (2) suy ra \(\dfrac{{AE}}{{AD}} = \dfrac{{BF}}{{BC}}\) \( \Rightarrow \dfrac{{ED}}{{AD}} + \dfrac{{BF}}{{BC}} = \dfrac{{ED}}{{AD}} + \dfrac{{AE}}{{AD}}\) \( = \dfrac{{ED + AE}}{{AD}} = \dfrac{{AD}}{{AD}} = 1\).
Do đó \(\dfrac{{ED}}{{AD}} + \dfrac{{BF}}{{BC}} = 1\) hay A đúng.
Cho tam giác \(ABC\), điểm \(D\) trên cạnh \(BC\) sao cho \(BD = \dfrac{3}{4}BC\), điểm \(E\) trên đoạn thẳng \(AD\) sao cho \(AE = \dfrac{1}{3}AD\). Gọi \(K\) là giao điểm của \(BE\) với \(AC\). Tỉ số \(\dfrac{{AK}}{{KC}}\) là:
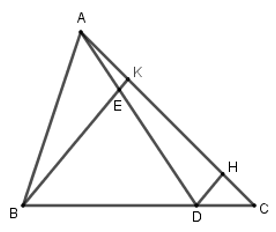
Qua \(D\) kẻ đường thẳng song song với \(BK\) cắt \(AC\) ở \(H\).
Theo định lí Ta-let:
Do \(EK//DH\) nên \(\dfrac{{AK}}{{KH}} = \dfrac{{AE}}{{ED}} = \dfrac{1}{2}\) (1)
Do \(DH//BK\) nên \(\dfrac{{KH}}{{KC}} = \dfrac{{BD}}{{BC}} = \dfrac{3}{4}\) (2)
Từ (1) và (2) suy ra \(\dfrac{{AK}}{{KH}}.\dfrac{{KH}}{{KC}} = \dfrac{1}{2}.\dfrac{3}{4} = \dfrac{3}{8}\).
Vậy \(\dfrac{{AK}}{{KC}} = \dfrac{3}{8}\).
Cho hình thang \(ABCD\)\(\left( {AB//CD} \right)\) có diện tích \(48\,c{m^2}\),\(AB = 4\,{\rm{cm,CD = 8}}\,{\rm{cm}}\). Gọi \(O\) là giao điểm của hai đường chéo. Tính diện tích tam giác \(COD\).
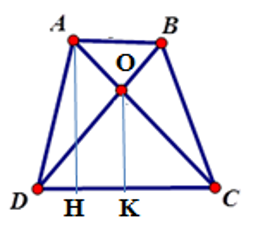
Kẻ \(AH \bot DC;\,OK \bot DC\) tại \(H;K\) suy ra \(AH{\rm{//}}OK\).
Chiều cao của hình thang: \(AH = \dfrac{{2{S_{ABCD}}}}{{AB + CD}} = \dfrac{{2.48}}{{4 + 8}} = 8\left( {cm} \right)\).
Vì \(AB{\rm{//}}DC\) (do \(ABCD\) là hình thang) nên theo định lý Ta-lét ta có:
\(\dfrac{{OC}}{{OA}} = \dfrac{{CD}}{{AB}} = \dfrac{8}{4} = 2\) \( \Rightarrow \dfrac{{OC}}{{OC + OA}} = \dfrac{2}{{2 + 1}} \Leftrightarrow \dfrac{{OC}}{{AC}} = \dfrac{2}{3}\).
Vì \(AH{\rm{//}}OK\) (cmt) nên theo định lý Ta-lét cho tam giác \(AHC\) ta có:
\(\dfrac{{OK}}{{AH}} = \dfrac{{OC}}{{AC}} = \dfrac{2}{3}\) \( \Rightarrow OK = \dfrac{2}{3}AH\) \( \Leftrightarrow OK = \dfrac{2}{3}.8 = \dfrac{{16}}{3}\,cm\).
Do đó \({S_{COD}} = \dfrac{1}{2}OK.DC = \dfrac{1}{2}.\dfrac{{16}}{3}.8 = \dfrac{{64}}{3}\left( {c{m^2}} \right)\).
Chọn khẳng định đúng nhất.
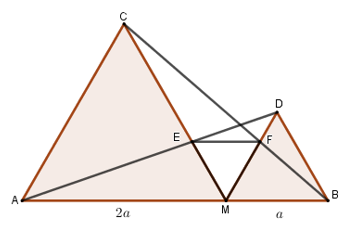
Từ câu a) ta có \(ME = MF \Rightarrow \Delta EMF\) cân tại \(M\). Ta lại có:
\(\widehat {EMF} = 180^\circ - \widehat {CMA} - \widehat {DMB}\)\( = 180^\circ - 60^\circ - 60^\circ = 60^\circ \)
Do đó \(MEF\) là tam giác đều (tam giác cân có một góc bằng \(60^\circ \)).
Vậy \(EF = ME = MF = \dfrac{{2a}}{3}\).
Đặt \(MB = a\). Tính \(ME,MF\) theo \(a\).
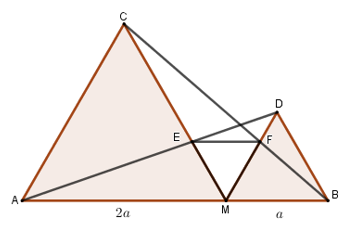
Đặt \(MB = a \Rightarrow MA = 2a\).
Vì các tam giác \(AMC\) và \(BMD\) đều nên \(\widehat {BMD} = \widehat {MAC} = 60^\circ \Rightarrow MD{\rm{//}}AC\) (vì hai góc ở vị trí đồng vị)
Vì \(MD{\rm{//}}AC\) nên theo hệ quả định lý Talet cho hai tam giác \(DEM\) và \(AEC\) ta có: \(\dfrac{{ME}}{{EC}} = \dfrac{{MD}}{{AC}} = \dfrac{{MB}}{{MA}} = \dfrac{1}{2}\)
Suy ra \(\dfrac{{ME}}{{EC}} = \dfrac{1}{2} \Rightarrow \dfrac{{ME}}{{ME + EC}} = \dfrac{1}{{1 + 2}} = \dfrac{1}{3}\) \( \Rightarrow \dfrac{{ME}}{{2a}} = \dfrac{1}{3} \Rightarrow ME = \dfrac{{2a}}{3}\)
Tương tự \(MF = \dfrac{{2a}}{3}\).
Vậy \(ME = MF = \dfrac{{2a}}{3}\).
Đặt \(MB = a\). Tính \(ME,MF\) theo \(a\).

Đặt \(MB = a \Rightarrow MA = 2a\).
Vì các tam giác \(AMC\) và \(BMD\) đều nên \(\widehat {BMD} = \widehat {MAC} = 60^\circ \Rightarrow MD{\rm{//}}AC\) (vì hai góc ở vị trí đồng vị)
Vì \(MD{\rm{//}}AC\) nên theo hệ quả định lý Talet cho hai tam giác \(DEM\) và \(AEC\) ta có: \(\dfrac{{ME}}{{EC}} = \dfrac{{MD}}{{AC}} = \dfrac{{MB}}{{MA}} = \dfrac{1}{2}\)
Suy ra \(\dfrac{{ME}}{{EC}} = \dfrac{1}{2} \Rightarrow \dfrac{{ME}}{{ME + EC}} = \dfrac{1}{{1 + 2}} = \dfrac{1}{3}\) \( \Rightarrow \dfrac{{ME}}{{2a}} = \dfrac{1}{3} \Rightarrow ME = \dfrac{{2a}}{3}\)
Tương tự \(MF = \dfrac{{2a}}{3}\).
Vậy \(ME = MF = \dfrac{{2a}}{3}\).
Đặt \(MA = a,MB = b\). Tính \(ME,MF\) theo \(a\) và \(b\).

Vì các tam giác \(AMC\) và \(BMD\) đều nên \(\widehat {BMD} = \widehat {MAC} = 60^\circ \Rightarrow MD{\rm{//}}AC\) (vì hai góc ở vị trí đồng vị)
Vì \(MD{\rm{//}}AC\) nên theo hệ quả định lý Talet cho hai tam giác \(DEM\) và \(AEC\) ta có \(\dfrac{{ME}}{{EC}} = \dfrac{{MD}}{{AC}} = \dfrac{b}{a}\)
Suy ra
\(\begin{array}{l}\dfrac{{ME}}{{EC}} = \dfrac{b}{a} \Rightarrow \dfrac{{ME}}{{ME + EC}} = \dfrac{b}{{b + a}}\\ \Rightarrow \dfrac{{ME}}{a} = \dfrac{b}{{b + a}} \Rightarrow ME = \dfrac{{ab}}{{b + a}}\end{array}\)
Tương tự \(MF = \dfrac{{ba}}{{a + b}}\) .
Vậy \(ME = MF = \dfrac{{ab}}{{b + a}}\).
Cho tứ giác \(ABCD\) có \(O\) là giao điểm hai đường chéo. Đường thẳng qua \(A\) và song song với \(BC\) cắt \(BD\) ở \(E\). Đường thẳng qua \(B\) và song song với \(AD\) cắt \(AC\) ở \(G\). Chọn kết luận sai?
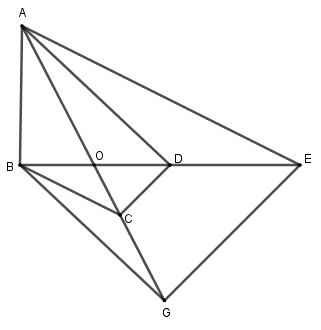
Theo định lí Ta-let:
Ta có: \(AE//BC\) nên \(\dfrac{{OE}}{{OB}} = \dfrac{{OA}}{{OC}}\) (1) hay A đúng.
\(BG//AD\) nên \(\dfrac{{OB}}{{OD}} = \dfrac{{OG}}{{OA}}\) (2) hay C đúng.
Từ (1) và (2) suy ra: \(\dfrac{{OE}}{{OB}}.\dfrac{{OB}}{{OD}} = \dfrac{{OA}}{{OC}}.\dfrac{{OG}}{{OA}}\) hay \(\dfrac{{OE}}{{OD}} = \dfrac{{OG}}{{OC}}\), do đó \(EG//CD\) (định lí Ta-let đảo) hay D đúng.
Vậy B sai.

