Có bao nhiêu nghiệm của đa thức \(h(x)\) với \(h(x)=f(x)-g(x)\).
Theo câu trước ta có: \(h(x)=f(x)-g(x)= {x^2} - x\)
Ta có: \(h(x) = 0 \Leftrightarrow {x^2} - x = 0\).
\( \Leftrightarrow x(x - 1) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\)
Vậy đa thức h(x) các các nghiệm là: \(x = 0;x = 1.\)
Tìm đa thức h(x) sao cho \(h(x) = f(x) - g(x)\).
\(h(x) = f(x) - g(x) = \)(\({x^4} + {x^3} - 3{x^2} + 2x - 4\))\( - ({x^4} + {x^3} - 4{x^2} + 3x - 4)\)
\( = {x^4} + {x^3} - 3{x^2} + 2x - 4\)\( - {x^4} - {x^3} + 4{x^2} - 2x + 4\)
\( = {x^2} - x\).
Vậy \(h\left( x \right) = {x^2} - x\).
Sắp xếp các đa thức \(f\left( x \right),\,{\rm{ }}g\left( x \right)\) theo lũy thừa giảm dần của biến.
Ta có: \(f(x) = - 3{x^2} + {x^4} + 2x + {x^3} - 4\)\( = {x^4} + {x^3} - 3{x^2} + 2x - 4\)
\(g(x) = {x^3} - 4{x^2} + {x^4} - 4 + 3x \)\(= {x^4} + {x^3} - 4{x^2} + 3x - 4\).
Vậy \(f\left( x \right) = {x^4} + {x^3} - 3{x^2} + 2x - 4;\) \(g\left( x \right) = {x^4} + {x^3} - 4{x^2} + 3x - 4.\)
Sắp xếp các đa thức \(f\left( x \right),\,{\rm{ }}g\left( x \right)\) theo lũy thừa giảm dần của biến.
Ta có: \(f(x) = - 3{x^2} + {x^4} + 2x + {x^3} - 4\)\( = {x^4} + {x^3} - 3{x^2} + 2x - 4\)
\(g(x) = {x^3} - 4{x^2} + {x^4} - 4 + 3x \)\(= {x^4} + {x^3} - 4{x^2} + 3x - 4\).
Vậy \(f\left( x \right) = {x^4} + {x^3} - 3{x^2} + 2x - 4;\) \(g\left( x \right) = {x^4} + {x^3} - 4{x^2} + 3x - 4.\)
Biết \(BE = 12cm;AD = 5cm\). Tính độ dài đoạn thẳng \(BD.\)
Áp dụng định lý Py-ta-go vào tam giác vuông BDE có:
\(B{D^2} = B{E^2} + D{E^2} \Leftrightarrow B{D^2} = BE{}^2 + A{D^2}\) (do \(AD = DE\) (theo câu trước))
\( \Leftrightarrow BD = \sqrt {B{E^2} + A{D^2}} = \sqrt {{{12}^2} + {5^2}} = \sqrt {169} = 13(cm)\).
So sánh độ dài các đoạn thẳng \(AD\) và \(DC\).
Do tam giác \(DEC\) vuông tại \(C\) nên \(DC > DE;\) mà \(DE = AD\) (theo câu trước)
Suy ra \(DC > AD.\)
Chọn câu đúng.
Xét hai tam giác vuông ABD và EBD có:
BD chung; \(\widehat {ABD} = \widehat {EBD}\) (gt)
\( \Rightarrow \Delta ABD = \Delta EBD \,(ch - gn)\)
\( \Rightarrow BA = BE;DA = DE\) (hai cạnh tương ứng)
Suy ra: \(\Delta ABE\) cân tại \(B\) và \(\Delta ADE\) cân tại D.
Chọn câu đúng.
Xét hai tam giác vuông ABD và EBD có:
BD chung; \(\widehat {ABD} = \widehat {EBD}\) (gt)
\( \Rightarrow \Delta ABD = \Delta EBD \,(ch - gn)\)
\( \Rightarrow BA = BE;DA = DE\) (hai cạnh tương ứng)
Suy ra: \(\Delta ABE\) cân tại \(B\) và \(\Delta ADE\) cân tại D.
Bậc của đa thức \({x^5} - 2{x^2}y - 2x + 9 - {x^5} - y\) là:
Đa thức \({x^5} - 2{x^2}y - 2x + 9 - {x^5} - y\)\( = \left( {{x^5} - {x^5}} \right) - 2{x^2}y - 2x - y + 9\) \( = - 2{x^2}y - 2x - y + 9\).
Bậc cao nhất của các hạng tử trong đa thức thu gọn trên là \(2 + 1 = 3.\)
Bậc của đa thức đã cho là \(3.\)
Cho tam giác \(ABC\) các đường phân giác \(AM\) của góc \(A\) và \(BN\) của góc \(B\) cắt nhau tại \(I\).
Khi đó, điểm \(I\):
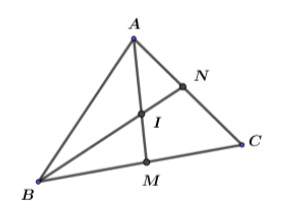
Cho tam giác \(ABC\) các đường phân giác \(AM\) của góc \(A\) và \(BN\) của góc \(B\) cắt nhau tại \(I\)
Khi đó, điểm \(I\) cách đều ba cạnh của tam giác.
Cho hình sau, biết \(G\) là trọng tâm của tam giác \(ABC\). Đẳng thức nào sau đây không đúng?
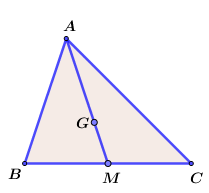
Quan sát hình vẽ và dựa vào tính chất ba đường trung tuyến của một tam giác đã học ta có: \(AG = \dfrac{2}{3}AM\)
\( + )\,\,\dfrac{{GM}}{{GA}} = \dfrac{1}{2}\) nên câu A đúng.
\( + )\,\,\dfrac{{AG}}{{AM}} = \dfrac{2}{3}\) nên câu B đúng.
\( + )\,\,\dfrac{{AG}}{{GM}} = \dfrac{2}{1} = 2\) nên câu C đúng.
\( + )\,\,\dfrac{{GM}}{{AM}} = \dfrac{1}{3}\) nên câu D sai.
Tích của hai đơn thức \(\left( { - 2x{y^3}} \right)\) và \({x^2}y\) là:
Ta có \(\left( { - 2x{y^3}} \right).\left( {{x^2}y} \right) = - 2.\left( {x.{x^2}} \right).\left( {{y^3}.y} \right)\) \( = - 2{x^3}{y^4}.\)
Tam giác \(ABC\) vuông tại A, kẻ \(AH \bot BC\) tại H. Biết \(\widehat {ABC} = {65^0}\). Số
đo \(\widehat {HAC}\) là:
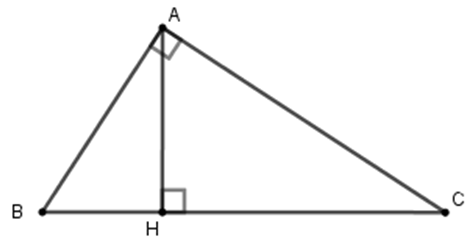
Xét tam giác \(AHB\) vuông tại \(H,\) có \(\widehat {BAH} + \widehat {ABH} = {90^0}\) mà \(\widehat {ABH} = \widehat {ABC} = {65^0}\)
Nên \(\widehat {BAH} = {90^0} - \widehat {ABH} = {90^0} - {65^0}\) \( = {25^0}\)
Lại có \(\widehat {BAH} + \widehat {HAC} = {90^0}\) nên \(\widehat {HAC} = {90^0} - \widehat {BAH} = {90^0} - {25^0}\) \( = {65^0}.\)
Vậy \(\widehat {HAC} = {65^0}.\)
Nếu \(\left| {x - 3,6} \right| = 1,4\) thì giá trị của \(x\) là:
Ta có \(\left| {x - 3,6} \right| = 1,4\)
TH1: \(x - 3,6 = 1,4\)
\(\begin{array}{l}x = 3,6 + 1,4\\x = 5\end{array}\)
TH2: \(x - 3,6 = - 1,4\)
\(x = 3,6 - 1,4\)
\(x = 2,2\)
Vậy \(x = 5;x = 2,2.\)
Tam giác \(DEF\) vuông tại \(D\) có \(DE = 5cm,{\rm{ }}EF = 13cm\) khi đó số đo cạnh DF bằng:
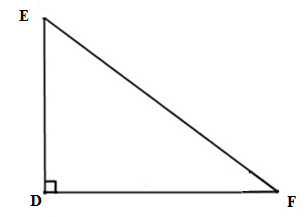
Xét tam giác \(DEF\) vuông tại \(D\), theo định lý Pytago ta có \(D{E^2} + D{F^2} = E{F^2} \Leftrightarrow D{F^2} = E{F^2} - D{E^2}\)
\( \Leftrightarrow D{F^2} = {13^2} - {5^2} = 144 \Rightarrow DF = 12\,cm\)
Vậy \(DF = 12\,cm.\)
Thu gọn đơn thức \(A = {\left( { - 2x{y^3}} \right)^2}.\dfrac{3}{8}x{z^2}\) rồi tìm bậc của đơn thức đó.
\(\begin{array}{l}A = {\left( { - 2x{y^3}} \right)^2}.\dfrac{3}{8}x{z^2}\\ = \left( { (- 2)^2.\dfrac{3}{8}} \right){\left( {x{y^3}} \right)^2}.x.{z^2}\\ = \dfrac{3}{2}{x^2}.{y^6}.x.{z^2}\\ = \dfrac{3}{2}{x^3}{y^6}{z^2}\end{array}\).
Vậy \(A = \dfrac{3}{2}{x^3}{y^6}{z^2}\).
Bậc của đơn thức: \(3 + 6 + 2 = 11\).
Kết quả của phép tính \(1\dfrac{4}{5} + \dfrac{6}{{29}} - \dfrac{4}{5} + \dfrac{{23}}{{29}}\) là:
Ta có:
\(1\dfrac{4}{5} + \dfrac{6}{{29}} - \dfrac{4}{5} + \dfrac{{23}}{{29}} = \left( {1\dfrac{4}{5} - \dfrac{4}{5}} \right) + \left( {\dfrac{6}{{29}} + \dfrac{{23}}{{29}}} \right)\)\( = 1 + 1 = 2\)
Tính hợp lý \(\dfrac{{ - 4}}{{13}}.\dfrac{5}{{17}} + \dfrac{{ - 12}}{{13}}.\dfrac{4}{{17}} + \dfrac{4}{{13}}\) ta được kết quả là:
Ta có \(\dfrac{{ - 4}}{{13}}.\dfrac{5}{{17}} + \dfrac{{ - 12}}{{13}}.\dfrac{4}{{17}} + \dfrac{4}{{13}}\)
\( = \dfrac{{ - 4}}{{13}}.\dfrac{5}{{17}} + \dfrac{{ - 4}}{{13}}.3.\dfrac{4}{{17}} + \dfrac{4}{{13}}\)
\( = \dfrac{{ - 4}}{{13}}.\dfrac{5}{{17}} + \dfrac{{ - 4}}{{13}}.\dfrac{{12}}{{17}} + \dfrac{4}{{13}}\)
\( = \dfrac{4}{{13}}\left( {\dfrac{{ - 5}}{{17}} + \dfrac{{ - 12}}{{17}} + 1} \right)\)
\( = \dfrac{4}{{17}}.( - 1 + 1) = \dfrac{4}{{17}}.0 = 0\)
Tìm x biết \(x + \dfrac{1}{3} = \dfrac{2}{5} - \left( { - \dfrac{1}{3}} \right)\)
Ta có:
\(x + \dfrac{1}{3} = \dfrac{2}{5} - \left( { - \dfrac{1}{3}} \right) \Leftrightarrow x + \dfrac{1}{3} = \dfrac{2}{5} + \dfrac{1}{3}\)\( \Leftrightarrow x = \dfrac{2}{5}\)
Vậy \(x = \dfrac{2}{5}.\)
Tìm \(x,{\rm{ }}y\) biết \(2x = 3y\) và \(3x + y = 33\)
Ta có: \(2x = 3y \Rightarrow \dfrac{x}{3} = \dfrac{y}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{3} = \dfrac{y}{2} = \dfrac{{3x + y}}{{9 + 2}} = \dfrac{{33}}{{11}} = 3\)
\( \Rightarrow x = 3.3 = 9; y = 2.3 = 6\)
Vậy \(x = 9;y = 6.\)

