Hình chóp tam giác đều có mặt bên là hình gì?
Hình chóp tam giác đều có các cạnh bên bằng nhau và các cạnh đáy bằng nhau nên mặt bên là những tam giác cân.
Hình chóp ngũ giác đều có bao nhiêu mặt?
Hình ngũ giác đều có \(5\) mặt bên và 1 mặt đáy nên có tất cả \(6\) mặt.
Diện tích xung quanh hình chóp đều được tính theo công thức:
Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy và trung đoạn.
Hình chóp đều có chiều cao \(h\), thể tích \(V\). Diện tích đáy \(S\) bằng:
\(V = \dfrac{1}{3}S.h\) nên \(S = \dfrac{{3V}}{h}\)
Tính diện tích toàn phần của hình chóp tứ giác đều.
Chu vi đáy bằng: \(48.4 = 192\left( {cm} \right)\)
\({S_{xq}} = p.d = \dfrac{{192}}{2}.10 = 960\left( {c{m^2}} \right)\)
Diện tích đáy bằng: \(48.48 = 2304\left( {c{m^2}} \right)\)
Diện tích toàn phần: \(960 + 2304 = 3264\left( {c{m^2}} \right)\)
Tính độ dài trung đoạn.
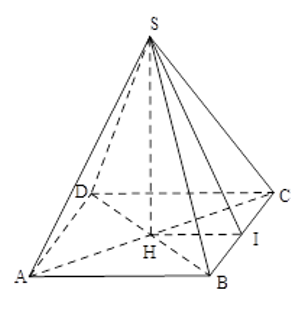
Xét hình chóp tứ giác đều \(S.ABCD\) có đường cao
\(SH = 10cm\), cạnh \(AB = 48cm\)
Gọi \(SI\) là đường cao của \(\Delta SBC\). Tam giác \(SBC\) cân tại \(S\) nên \(BI = IC\). Ta có: \(HI\) là đường trung bình của \(\Delta ABC\)nên \(HI = \dfrac{{AB}}{2} = \dfrac{{48}}{2} = 24\left( {cm} \right)\)
Áp dụng định lí Py-ta-go vào tam giác vuông \(SHI\). Ta có: \(S{I^2} = S{H^2} + H{I^2} = {10^2} + {24^2} = 676 = {26^2}\).
Nên \(SI = 26\left( {cm} \right)\).
Tính độ dài trung đoạn.

Xét hình chóp tứ giác đều \(S.ABCD\) có đường cao
\(SH = 10cm\), cạnh \(AB = 48cm\)
Gọi \(SI\) là đường cao của \(\Delta SBC\). Tam giác \(SBC\) cân tại \(S\) nên \(BI = IC\). Ta có: \(HI\) là đường trung bình của \(\Delta ABC\)nên \(HI = \dfrac{{AB}}{2} = \dfrac{{48}}{2} = 24\left( {cm} \right)\)
Áp dụng định lí Py-ta-go vào tam giác vuông \(SHI\). Ta có: \(S{I^2} = S{H^2} + H{I^2} = {10^2} + {24^2} = 676 = {26^2}\).
Nên \(SI = 26\left( {cm} \right)\).
Một hình chóp tứ giác đều có thể tích bằng \(64\,c{m^3}\), chiều cao bằng \(12\,cm\). Tính độ dài cạnh đáy.
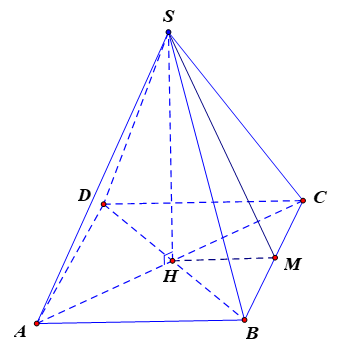
Xét hình chóp tứ giác đều \(S.ABCD\) có: \(V = 64c{m^3}\), chiều cao $h=12cm$.
Ta có: \(V = \dfrac{1}{3}{S_d}.h \Rightarrow \) \({S_d} = \dfrac{{3V}}{{SH}} = \dfrac{{3.64}}{{12}} = 16\left( {c{m^2}} \right)\)
Tức là \(B{C^2} = 16 \Rightarrow BC = 4\)
Vậy độ dài cạnh đáy là \(4\,cm\).
Thể tích của hình chóp tứ giác đều có chiều cao \(9\) cm, cạnh đáy \(5\) cm là:
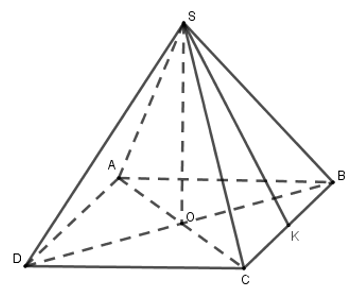
Đáy của chóp tứ giác đều là hình vuông nên diện tích đáy là: \(S = {5^2} = 25\,c{m^2}\).
Thể tích cần tìm là: \(V = \dfrac{1}{3}.9.25 = 75\,c{m^3}\).
Tính diện tích xung quanh của hình chóp cụt tứ giác đều có các cạnh đáy bằng \(10cm\) và \(15cm\), chiều cao của mặt bên bằng \(12cm\).
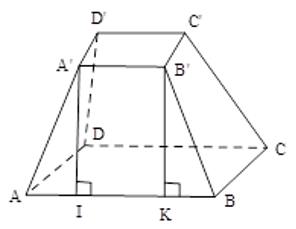
Mặt bên hình chóp cụt tứ giác đều là hình thang cân nên diện tích một mặt bên bằng \(\dfrac{{\left( {10 + 15} \right).12}}{2} = 150\,(c{m^2})\).
Hình chóp cụt tứ giác đều có \(4\)mặt bên bằng nhau nên diện tích xung quanh bằng \(150.4 = 600\left( {c{m^2}} \right)\).
Tính diện tích xung quanh hình chóp (làm tròn đến một chữ số thập phân)
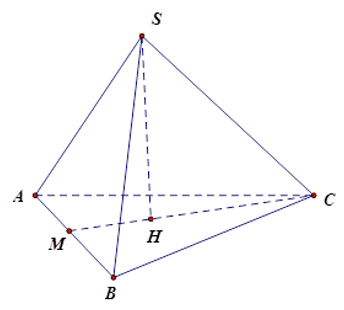
Xét tam giác \(SAB\) và \(CAB\) là hai tam giác đều có cạnh bằng nhau nên \(SM = CM\).
\( \Rightarrow SM = CM = \dfrac{{9\sqrt 3 }}{2}\) cm
\({S_{xq}} = pd = \dfrac{{9.3}}{2}.\dfrac{{9\sqrt 3 }}{2} \approx 105,2\left( {c{m^2}} \right)\).
Độ dài cạnh hình chóp là:
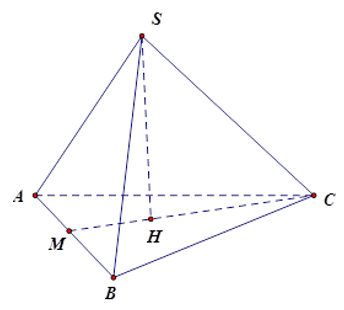
Gọi \(M\) là giao điểm của \(CH\) và \(AB\) ta có: \(CM \bot AB\) và \(AM = MB\).
Vì \(H\) là trọng tâm \(\Delta ABC\) nên \(CM = \dfrac{3}{2}CH = \dfrac{3}{2}.3\sqrt 3 = \dfrac{{9\sqrt 3 }}{2}(cm)\)
Đặt \(AB = BC = x\), ta có: \(B{C^2} - M{B^2} = C{M^2}\) (định lý Pytago cho \(\Delta MBC\)) nên
\({x^2} - {\left( {\dfrac{x}{2}} \right)^2} = {\left( {\dfrac{{9\sqrt 3 }}{2}} \right)^2}\) \( \Leftrightarrow \dfrac{{3{x^2}}}{4} = \dfrac{{243}}{4} \Leftrightarrow {x^2} = 81 \Leftrightarrow x = 9\)
Vậy các cạnh của hình chóp có độ dài là \(9cm\).
Độ dài cạnh hình chóp là:

Gọi \(M\) là giao điểm của \(CH\) và \(AB\) ta có: \(CM \bot AB\) và \(AM = MB\).
Vì \(H\) là trọng tâm \(\Delta ABC\) nên \(CM = \dfrac{3}{2}CH = \dfrac{3}{2}.3\sqrt 3 = \dfrac{{9\sqrt 3 }}{2}(cm)\)
Đặt \(AB = BC = x\), ta có: \(B{C^2} - M{B^2} = C{M^2}\) (định lý Pytago cho \(\Delta MBC\)) nên
\({x^2} - {\left( {\dfrac{x}{2}} \right)^2} = {\left( {\dfrac{{9\sqrt 3 }}{2}} \right)^2}\) \( \Leftrightarrow \dfrac{{3{x^2}}}{4} = \dfrac{{243}}{4} \Leftrightarrow {x^2} = 81 \Leftrightarrow x = 9\)
Vậy các cạnh của hình chóp có độ dài là \(9cm\).
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng \(6\,cm\). Thể tích hình chóp gần nhất với số nào dưới đây?
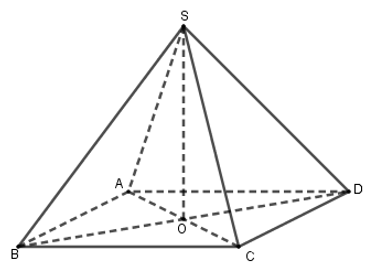
Diện tích đáy: \({S_{ABCD}} = {6^2} = 36\left( {c{m^2}} \right)\).
Xét tam giác \(ABC\) có: \(A{C^2} = A{B^2} + B{C^2} = {6^2} + {6^2} = 72\) \( \Rightarrow AC \approx 8,5\)\( \Rightarrow AO = \dfrac{1}{2}AC = 4,25\)
Tam giác \(SOA\) vuông tại \(O\) có: \(S{A^2} = S{O^2} + O{A^2}\) \( \Leftrightarrow {6^2} = S{O^2} + 4,{25^2}\) \( \Leftrightarrow SO = 4,25\)
Thể tích hình chóp: \(V = \dfrac{1}{3}{S_{ABCD}}.SO = \dfrac{1}{3}.36.4,25 = 51\left( {c{m^3}} \right)\).
Tính thể tích của hình chóp cụt \(ABCD.A'B'C'D'\).
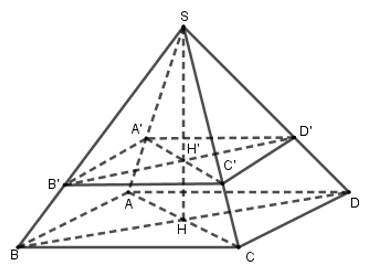
Ta có: \(SH' = \dfrac{2}{3}SH = \dfrac{2}{3}.6 = 4\,cm\)
Xét tam giác \(SAH\) có: \(A'H'//AH\) và \(\dfrac{{SH'}}{{SH}} = \dfrac{2}{3}\) \( \Rightarrow \dfrac{{SA'}}{{SA}} = \dfrac{2}{3}\) (định lí Ta let)
Mà \(A'B'//AB\) \( \Rightarrow \dfrac{{A'B'}}{{AB}} = \dfrac{{SA'}}{{SA}} = \dfrac{2}{3}\) \( \Rightarrow A'B' = \dfrac{2}{3}AB = \dfrac{2}{3}.6 = 4\)
Thể tích hình chóp \(S.A'B'C'D'\) bằng: \(\dfrac{1}{3}{.4^2}.4 = \dfrac{{64}}{3}\,c{m^3}\)
Thể tích hình chóp cụt bằng: \(72 - \dfrac{{64}}{3} = \dfrac{{152}}{3}\,c{m^3}\).
Tính thể tích của hình chóp \(S.ABCD\).
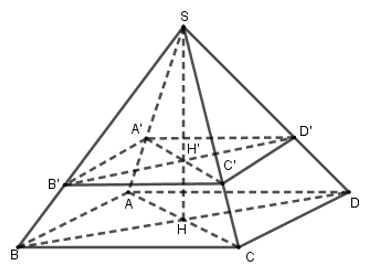
Thể tích hình chóp bằng: \(\dfrac{1}{3}{.6^2}.6 = 72\,c{m^3}\).
Tính thể tích của hình chóp \(S.ABCD\).

Thể tích hình chóp bằng: \(\dfrac{1}{3}{.6^2}.6 = 72\,c{m^3}\).
Tính độ dài trung đoạn.
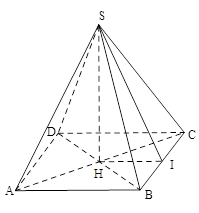
Xét hình chóp tứ giác đều $S.ABCD$ có đường cao
$SH = 35cm$, cạnh $AB = 24cm\,\,$
Gọi $SI$ là đường cao của $\Delta SBC$. Tam giác $SBC$ cân tại $S$ nên $BI = IC$ . Ta có $HI$ là đương trung bình của $\Delta ABC$nên $HI = \dfrac{{AB}}{2} = \dfrac{{24}}{2} = 12\left( {cm} \right)$
Áp dụng định lí Py-ta-go vào tam giác vuông $SHI$ Ta có $S{I^2} = S{H^2} + H{I^2} = {35^2} + {12^2} = 1369 = {37^2}$
Nên $SI = 37\left( {cm} \right)$.
Tính \(AB\) .
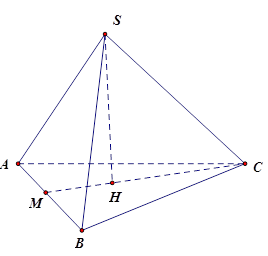
Gọi $M$ là giao điểm của $CH$ và $AB$ ta có \(CM \bot AB\) và $AM = BM$ . Vì \(H\) là trọng tâm \(\Delta ABC\) nên
\(CM = \dfrac{3}{2}CH = \dfrac{3}{2}.2\sqrt 3 = 3\sqrt 3 (cm)\)
Đặt $AB = BC = x$ , ta có \(B{C^2} - M{B^2} = C{M^2}\) (định lý Pytago cho \(\Delta MBC\) ) nên
\({x^2} - {\left( {\dfrac{x}{2}} \right)^2} = {\left( {3\sqrt 3 } \right)^2}hay{\rm{ }}\dfrac{{3{x^2}}}{4} = 27\)
Suy ra $x = 6$ . Vậy $AB = 6cm$ .
Tính thể tích của hình chóp $S.ABCD$.
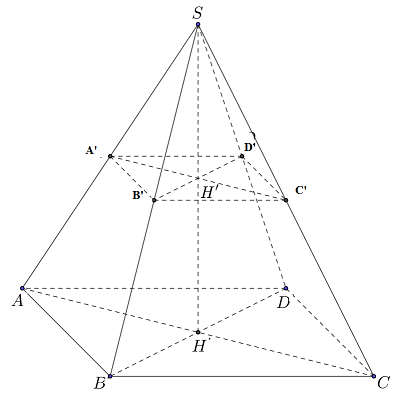
Thể tích hình chóp $S.ABCD$ bằng \(\dfrac{1}{3}{.4^2}.6 = 32\,c{m^3}\) .

